Presná definícia vektora, používaná v algebre, hovorí o n-tici čísel, ktorá sa istým definovaným spôsobom transformuje pri zmene súradnicovej sústavy. Pre naše účely vystačíme s konštatovaním, že vektorovej veličine vieme okrem veľkosti priradiť aj smer v priestore. 

Vektory zapisujeme tučnými písmenami, napr.  a, E, r, alebo ich označujeme šípkou nad písmenom.  Značky všetkých veličín, teda aj vektorových, sa podľa normy STN ISO 31-0 majú písať ležatým písmom - kurzívou.

Veľkosť vektorových veličín sa zapisuje jednoduchým písmom (nie tučným, resp. bez šípky nad písmenom):  b, E, f alebo sa vektor vloží medzi značky vyjadrujúce absolútnu hodnotu: |a|, |E|, |f|. Veľkosť vektora sa nazýva aj  absolútna hodnota,  je vždy nezáporná. Graficky sa vektorové veličiny znázorňujú úsečkou, so šípkou na jednom konci úsečky. 
 

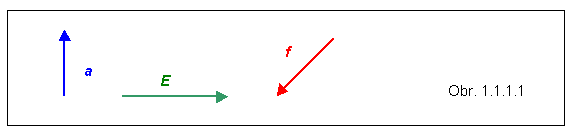
Miesto na úsečke opatrené šípkou sa považuje za "koniec vektora", na opačnej strane úsečky je "začiatok vektora".

Vektory rovnobežné s jednou priamkou nazývame kolineárne, vektory rovnobežné s jednou rovinou komplanárne. Kolineárne vektory môžu mať rovnaký, alebo navzájom opačný smer.

Dva vektory považujeme za rovnaké, ak majú rovnaký smer a rovnakú veľkosť  (sú teda kolineárne).
 

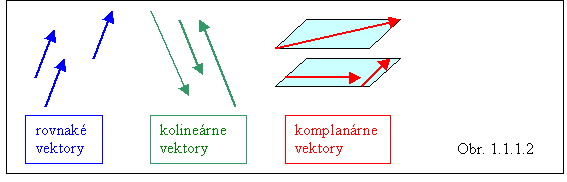
Kontrolné otázky

1. Ako označujeme vektory a ako ich veľkosti ?
2. Čo je absolútna hodnota vektora ?
3. Dva vektory, ktoré majú rovnakú veľkosť a rovnaký smer, nemajú spoločný začiatočný bod. Sú takéto vektory rovnaké ?
4. Dva rovnobežné vektory majú vzájomne opačný smer. Sú kolineárne ?
5. Kedy sú vektory komplanárne ?
6. Možno o dvoch rovnobežných vektoroch tvrdiť že sú komplanárne ?