 Súčet a rozdiel vektorov
Súčet a rozdiel vektorov
Súčet dvoch vektorov a + b = c je operácia, ktorej výsledkom je opäť vektor. Graficky sa znázorňuje pomocou úsečiek zobrazujúcich vektory: ku koncu prvého vektora pripojíme druhý vektor, pričom výsledkom ich sčítania je tretí vektor, ktorého začiatok je zhodný so začiatkom prvého vektora a koniec s koncom druhého vektora . V grafickom znázornení
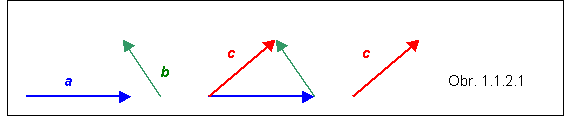
Analogicky sa pokračuje pri sčítaní viacerých vektorov. Súčet vektorov je komutatívna operácia, čiže výsledok súčtu nezávisí od poradia skladania vektorov:
a + b = b + a (1.1.2.1)
Pri sčítaní viacerých vektorov sa uplatňuje asociatívnosť, ktorú v prípade troch vektorov možno vyjadriť vzťahom
a + b + c = (a + b) + c = a + (b + c) (1.1.2.2)
Ak pred vektor napíšeme znamienko "mínus", napríklad - a , podľa zaužívanej dohody to predstavuje vektor, ktorý má rovnakú veľkosť ako vektor a , ale má opačný smer. Nový vektor možno označiť ako vektor b, a zapísať rovnosť b = - a . Vektory a , b sú teda kolineárne.
Takéto označenie umožňuje zaviesť odčítanie (rozdiel) vektorov. Rozdiel dvoch vektorov c - d = f chápeme ako súčet vektorov c a (- d), t.j. f = c + (- d) . Pritom rovnicu c - d = f možno upraviť rovnako, ako rovnicu s obyčajnými číslami, napríklad vektor d previesť na pravú stranu rovnice : c = d + f . Takto upravená rovnica môže poslúžiť na overenie správnosti vykonanej operácie.
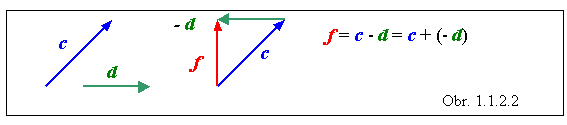
Na súčte vektorov si možno názorne ukázať význam používania vektorového označovania. Ak pri súčte dvoch vektorov platí rovnosť a + b = c , kde a , b nie sú kolineárne vektory, potom pre ich veľkosti platí trojuholníková nerovnosť a + b > c. Keby sme vynechali označenie vektorov, napísali by sme nesprávnu rovnicu a + b = c . Dôsledné používanie označovania vektorov je preto veľmi dôležité.
Príklad 1.1.2.1
Dva nekolineárne vektory, napr. a, b , môžeme chápať ako strany rovnobežníka. Graficky ukážte, že ich súčet a rozdiel predstavujú uhlopriečky tohto rovnobežníka.
Riešenie
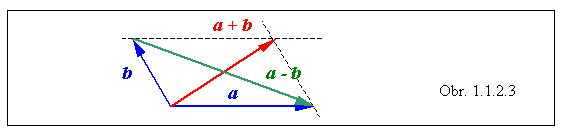
Súčet vektorov má časté uplatnenie v praxi. Napríklad sčítaním vektora rýchlosti lode vzhľadom na vodu s vektorom rýchlosti vody v rieke, dostaneme vektor rýchlosti lode vzhľadom na breh rieky.
Príklad 1.1.2.2
Nakreslite štvoruholník, ktorého strany nie sú rovnako dlhé. Dokážte, že ak by sa uhlopriečky štvoruholníka pretínali vo svojich stredoch, musel by to byť rovnobežník. (Obr. 1.1.2.4)
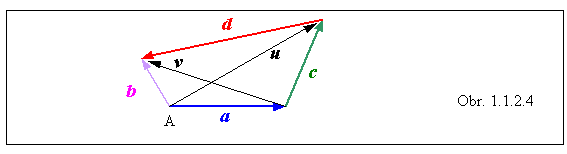
Riešenie
Najprv treba označiť všetky štyri strany štvoruholníka ako vektory. Podľa obrázku dokážeme určiť vektory smerujúce z vrcholu A do stredov uhlopriečok. Do stredu uhlopriečky u smeruje vektor p = (1/2) u = (1/2)(a + c) a do stredu uhlopriečky v vektor q = a + (1/2)(b - a) = (1/2)(a + b) . Ak majú byť stredy uhlopriečok totožné, musia byť vektory p a q rovnaké : (1/2)(a + c) = (1/2)(a + b) , z čoho bezprostredne vyplýva rovnosť vektorov b a c . Majú teda rovnakú veľkosť aj smer, preto sú rovnobežné, tvoria dve strany rovnobežníka. Výsledok pre ďalšie dve strany získame úvahou o vektore u. Platí u = c + a a súčasne u + d = b, čiže u = b - d a s využitím rovnosti b = c aj u = c - d . Porovnaním dvoch vyjadrení vektora u dospejeme k výsledku a = - d . Teda aj tieto vektory sú rovnobežné, majú rovnakú veľkosť, ale opačný smer.
Kontrolné otázky
- Slovne vyjadrite postup pri grafickom sčítaní dvoch vektorov
- Ovplyvní zámena poradia vektorov pri súčte výsledok ?
- Je sčítanie dvoch vektorov komutatívna operácia ?
- Je sčítanie viacerých vektorov asociatívna operácia ?
- Na príklade názorne vysvetlite asociatívnosť súčtu vektorov !
- Čo znamená znamienko mínus pred vektorom ?
- Ako je definované odčítanie dvoch vektorov ?
- K akým dôsledkom môže viesť nepoužívanie označenia vektorov ?
- Uveďte príklad z praxe, kde sa uplatňuje sčítanie vektorov !
