 Skalárny násobok vektora, jednotkový vektor
Skalárny násobok vektora, jednotkový vektor
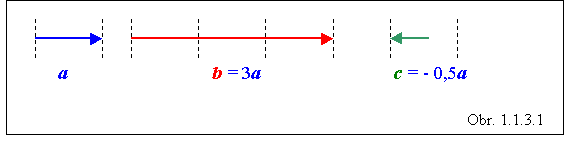
Násobenie vektora číslom je operácia, ktorá poskytne nový vektor so zmenenou veľkosťou, ale kolineárny s pôvodným vektorom. Napríklad vynásobením vektora a číslom 3 získame vektor b s trojnásobnou veľkosťou a nezmeneným smerom. Ak však vektor a budeme násobiť číslom - 0,5 , dostaneme vektor c s polovičnou veľkosťou, navyše s opačným smerom. Je to ďalšie pravidlo vektorovej algebry. Všeobecne tento vzťah zapisujeme v tvare
b = sa (1.1.3.1)
kde s môže predstavovať nie iba bezrozmerné číslo, ale aj skalárnu veličinu. Napríklad v kinematike sa stretneme s výrazom at , teda súčinom vektora zrýchlenia a času. Tak dostaneme novú fyzikálnu veličinu, ktorej veľkosť a fyzikálny rozmer sú súčinom veľkostí, resp. rozmerov vektorovej a skalárnej veličiny. V literatúre o vektorovom počte sa táto operácia nazýva skalárny násobok vektora.
Jednotkový vektor má veľkosť rovnajúcu sa číslu 1, je bezrozmerný. S výhodou ho možno použiť na vyjadrenie viacerých vektorov, ktoré sú s ním rovnobežné. Nech j je jednotkový vektor, a nech vektory a, b, c sú s ním súhlasne rovnobežné. Preto ich možno vyjadriť ako skalárne násobky jednotkového vektora, pričom skalármi, ktorými jednotkový vektor násobíme, sú veľkosti týchto vektorov : a = a j , b = b j , c = c j. Situácia sa môže skomplikovať, ak niektorý z vektorov má opačný smer ako jednotkový vektor. Vtedy pred skalárny násobok vektora j treba pripísať znamienko "mínus", napr. f = -3 j. (Pozri ďalej - rozklad vektora, súradnice vektora).
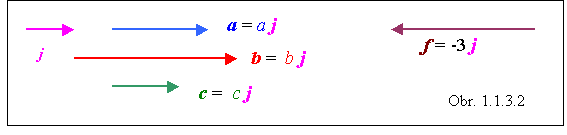
Kontrolné otázky
- Ako možno z daného vektora vytvoriť vektor opačného smeru, navyše s päťnásobnou veľkosťou ? Ako sa príslušná operácia nazýva ?
- Aké vlastnosti má jednotkový vektor ?
- Získame súčtom dvoch vzájomne kolmých jednotkových vektorov opäť jednotkový vektor ?
