 Skalárny súčin
Skalárny súčin
Vektorová algebra popri násobení vektorov skalármi zavádza aj súčiny medzi vektormi. Skalárny súčin dvoch vektorov je zavedený ako operácia, ktorej výsledkom je skalárna veličina. Hodnota tejto skalárnej veličiny je určená súčinom veľkostí príslušných vektorov a kosínusu uhla, ktorý tieto vektory zvierajú. Fyzikálny rozmer výslednej skalárnej veličiny sa rovná súčinu rozmerov násobených vektorových veličín. Skalárny súčin sa označuje bodkou medzi vektormi, v strede výšky písmen (nie na úrovni riadku) :
a × b = ab cos a (1.2.1.1)
Pritom uhol medzi dvoma vektormi sa určuje tak, aby nebol väčší ako p radiánov (180 o). Bezpečne ho určíme tak, keď oba vektory nakreslíme so spoločným začiatkom.
Niektoré vlastnosti skalárneho súčinu
- Skalárny súčin je komutatívny, čo vyplýva bezprostredne z jeho definície: a × b = b × a (1.2.1.2)
- Skalárny súčin môže byť kladný i záporný, čo závisí od hodnoty uhla medzi vektormi. Ak je uhol medzi vektormi menší ako p/2, skalárny súčin je kladný, lebo kosínus ostrého uhla je kladný. Pri uhle väčšom ako p/2, je kosínus uhla, a teda aj skalárny súčin, záporný.
- Ak sa skalárny súčin dvoch vektorov rovná nule, pričom ani jeden z vektorov nemá nulovú veľkosť, vektory sú na seba kolmé, lebo cos (p/2) = 0.
- Skalárny súčin vektora so sebou samým: a × a = aa cos 0 = a2 . V tomto prípade sa používa aj označenie a × a = a2.
- Pre skalárne súčiny medzi jednotkovými vektormi i, j, k karteziánskej súradnicovej sústavy platia vzťahy
i × i = 1 , j × j = 1 , k × k = 1 , i × j = 0 , i × k = 0, j × k = 0 (1.2.1.3)
- Pre skalárny súčin platí distributívny zákon:
a × (b + c) = a × b + a × c (1.2.1.4)
alebo všeobecnejšie:
(a1 + a2 + … + ap) × (b1 + b2 + …+ bq) = a1 × b1 + a1 × b2 +…+ a1× bq + … + ap × bq
- Skalárny súčin vektorov vyjadrených pomocou súradníc, teda ako lineárna kombinácia vektorov i, j, k, možno vypočítať s využitím distributívneho zákona takto:
a × b = (ax i + ay j + az k) × (bx i + by j + bz k ) = ax bx + ay by + az bz (1.2.1.5)
napríklad (3 i + 2 j - k) × (- i + 2 j - 2 k ) = -3 + 4 + 2 = 3.
- Z definície skalárneho súčinu vyplýva vzťah
takže porovnaním (1.2.5) a (1.2.6) môžeme získať vzorec na výpočet (kosínusu) uhla medzi vektormi:
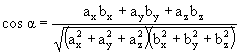 (1.2.1.7)
(1.2.1.7)-
Skalárny súčin možno využiť na výpočet súradnice vektora v karteziánskej sústave, ak vektor vynásobíme príslušným jednotkovým vektorom. Použitím distributívneho zákona (1.2.1.4) a vzťahov (1.2.1.3) dostaneme napríklad j × (ax i + ay j + az k) = ay . Podobne získame ostatné súradnice, takže platí:
ax = a × i, ay = a × j, az = a × k (1.2.1.8)
- Pomocou týchto vzťahov možno vytvoriť zložky vektora a v smere súradnicových osí v karteziánskej sústave, t.j. rozložiť ho na tieto zložky. Ide vlastne o ortogonálne priemety s , t a u vektora a do smerov súradnicových osí, t.j. do smerov určených jednotkovými vektormi i, j, k . Platí pre ne:
s = ax i = (a × i) i, t = ay j = (a × j) j, u = az k = (a × k) k (1.2.1.9)
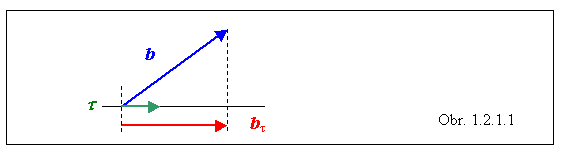
Tento postup môže poslúžiť aj pri vytváraní ortogonálneho priemetu vektora do ľubovoľného smeru v priestore, určeného jednotkovým vektorom. Napríklad priemet bt vektora b do smeru jednotkového vektora t (obr. 1.2.1.1 ) získame tak, že vypočítame ich skalárny súčin a takto získaným skalárom vynásobíme vektor t:
bt = (b × t)t (1.2.1.10)
Skalárny súčin sa často využíva v mechanike, a teórii elektromagnetického poľa. Napríklad skalárnym súčinom vektora sily f a vektora elementárneho posunutia dr sa vyjadruje elementárna práca dW = f × dr = f dr cos a , lebo smer sily a smer posunutia telesa nemusia byť rovnaké. Vtedy sa na vykonanie práce využíva iba priemet sily do smeru posunutia, vyjadrený ako f cosa.
Príklad 1.2.1.1
Na obr.1.2.1.2 je znázornený trojuholník určený vektormi a = 5i , b = 4i + 3j . Vypočítajte uhly medzi stranami a , b a stranami a, c .
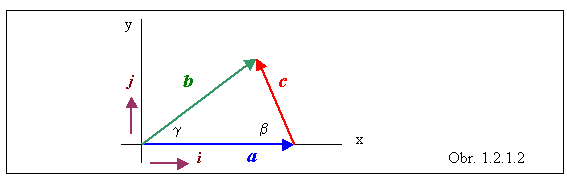
Riešenie
Na výpočet použijeme vzorec (1.2.1.7):
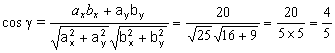
čiže g = 36,9o . Na výpočet uhla b potrebujeme vyjadriť vektor c = b - a = -i + 3j a opäť použiť vzorec (1.2.1.7) . Musíme si však uvedomiť, že vektor a s vektorom c zviera uhol j = 180o - b . Tak dostaneme: cos j = -1/sqrt(10) , čiže j = 108,43 o .
Kontrolné otázky
- Poznáme veľkosť dvoch vektorov a uhol medzi nimi. Čomu sa rovná ich skalárny súčin ?
- Aká je dohoda o maximálnej hodnote uhla medzi dvoma vektormi ?
- Kedy je skalárny súčin dvoch vektorov záporný ?
- Čomu sa rovná skalárny súčin vzájomne kolmých vektorov ?
- Uveďte, čomu sa rovnajú skalárne súčiny j × j a i × k !
- Viete vyjadriť skalárny súčin dvoch vektorov, ak poznáte ich súradnice v karteziánskej sústave ?
- Ako vyjadrujeme distributívnosť skalárneho súčinu ?
- Ako možno pomocou skalárneho súčinu vypočítať uhol medzi dvomi vektormi ?
- Čo rozumieme pod priemetom vektora do iného, s ním nekolineárneho vektora ?
- Čo predstavuje priemet vektora do jednotkového vektora v smere súradnicovej osi ?
