Vektorový súčinVektorový súčin

Vektorový súčin dvoch vektorov je zavedený ako operácia, ktorej výsledkom je vektor. Preto treba definovať nie iba veľkosť výsledku, ale aj smer výsledného vektora. Vektorový súčin sa označuje krížikom  medzi vektormi:
 
c  =  a ´ b        (1.2.2.1)
 
Veľkosť  c  výsledného vektora  c  je definovaná ako súčin veľkostí násobených vektorov a sínusu uhla nimi zovretého:            
 
c  =  ab sina        (1.2.2.2)
 
 Pre smer vektora  c platí definícia, že je kolmý na rovinu násobených vektorov. Jednoznačnosť definície však vyžaduje určiť, na ktorú stranu roviny smeruje. Vektor  c  má taký smer, že z jeho konca sa stotožnenie prvého vektora zo súčinu  (v tomto prípade vektora  a) s druhým vektorom po kratšom oblúku javí ako pohyb proti chodu hodinových ručičiek. O trojici vektorov a, b, c v danom poradí potom hovoríme, že tvoria pravotočivú sústavu vektorov. Zmena ich poradia jednou permutáciou znamená zmenu z  pravotočivej na ľavotočivú sústavu (trojicu).
 
 
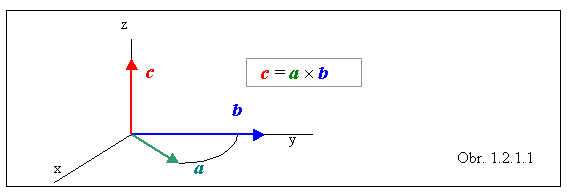
Na obr. 1.2.1.1 je trojica vektorov   a , b , c  znázornená v axonometrickom pohľade. Pre názornosť sú nakreslené aj súradnicové osi karteziánskej sústavy, vektor  a  leží v rovine (x,y). Vektor  a  budeme otáčať smerom k vektoru  b  po kratšom oblúku. Ak rovnako budeme otáčať pravotočivú skrutku, umiestnenú v začiatku súradnicovej sústavy - kolmo na rovinu vektorov (a , b) - skrutka sa bude posúvať v smere vektora c . Aj tento model pomáha pri určovaní smeru vektora, ktorý je výsledkom vektorového súčinu.
 
Niektoré vlastnosti vektorového súčinu
  • Vektorový súčin nie je komutatívna operácia, lebo zámena poradia vektorov poskytuje síce vektor rovnako veľký, ale opačného smeru. Táto skutočnosť sa zapisuje v tvare
a ´ b  =  -  b ´ a        (1.2.2.3)
  • Veľkosť vektorového súčinu dvoch vektorov možno interpretovať ako plošný obsah rovnobežníka vytvoreného týmito vektormi. Navyše výsledný vektor jednoznačne určuje  orientáciu roviny v priestore, preto ho možno chápať ako vektor priradený ploche.
  • Z definície veľkosti vektorového súčinu vyplýva, že vektorový súčin dvoch kolineárnych vektorov sa rovná nule (je nulový vektor).
  • Pre jednotkové vektory  i ,  j , k  , ktoré sú navzájom na seba kolmé, platia vzťahy:
i ´ i = 0                j ´ j = 0                k ´ k = 0
i ´ j = k          j ´ k = i           k ´ i  = j          j ´ i = - k          k ´ j = - i         i ´ k = -j      (1.2.2.4)
  • Pre vektorový súčin platí distributívny zákon:

 a ´ (b + c) =  a ´ b   +  a ´ c               (b + c) ´ a  =  b ´ a   +  c ´ a       (1.2.2.5)       

Dva prípady distributívneho zákona sú uvedené preto, lebo vo vektorovom súčine nemožno zamieňať poradie vektorov bez zmeny znamienka.
  • Na základe distributívneho zákona vektorový súčin vektorov vyjadrených v zložkovom tvare môžeme vyjadriť nasledovne :
                                        a ´ b  =      (ax i + ay j + az k) ´ (bx i + by j + bz k )     =
                                                        =       axbx(i ´ i) + axby(i ´ j)  + axbz(i ´ k)    +
                                                                + aybx(j ´ i)  + ayby(j ´ j)  + aybz( j ´ k)    +
                                                                + azbx(k ´ i) + azby(k ´ j) + az bz(k ´ k)   =   
                                                        =           0               +  axby k        -  axbz j           +
                                                                - aybx k         +     0           +  aybz i           +
                                                                + azbx j         -  azby i        +     0               =
                                                        =      i (aybz  -  azby ) 
                                                                +  j (azbx - axbz ) 
                                                                +  k (axby -  aybx )        (1.2.2.6)
Čitateľovi, ktorý pozná determinanty je zrejmé, že posledný výraz možno formálne vyjadriť  ako determinant:
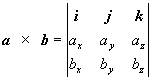        (1.2.2.7)
 
S vektorovým súčinom sa stretneme napríklad pri vyjadrení momentu sily  M = r  ´ f, kde  r je polohový vektor pôsobiska sily  f ,  alebo pri vzťahu pre silu  f  pôsobiacu na elektrický náboj  q  pohybujúci sa v magnetickom poli s magnetickou indukciou  B :      f  = qv ´ B .
                                                                                                              
 
Príklad  1.2.2.1 
Určte plošný obsah trojuholníka určeného vektormi  a = 5 i  a  b = 4 i + 3 j  . (Pozri príklad 1.2.1.1 , kde je obrázok)
 
Riešenie
Veľkosť vektorového súčinu  a ´ b  predstavuje plošný obsah rovnobežníka vytvoreného pomocou týchto vektorov, plošný obsah trojuholníka je jeho polovicou. Mohli by sme postupovať tak, že vypočítame veľkosti  vektorov  a, b a uhol medzi nimi (pomocou vzorca (1.2.1.7)) , vypočítame veľkosť vektorového súčinu ab sina  a vydelíme ho dvomi. Pri šikovnejšom postupe najprv vypočítame výsledný vektor  u = a ´ b  :
u = (5 i) ´ (4 i + 3 j ) =  (5 × 4)(i ´ i) + (5 × 3)(i ´ j)  =  15 k,
 
a z výsledku bezprostredne vidíme, že veľkosť vektora  u  je  15. Preto plošný obsah trojuholníka je  7,5  jednotiek.
 
 
Príklad 1.2.2.2
V priestore sú zadané tri body  A(2,0,0),  B(0,1,0),  C(0,0,3) , ktorými je určená rovina. Vyjadrite jednotkový vektor kolmý na túto rovinu. Nakreslite si obrázok !
 
Riešenie
Základnou myšlienkou riešenia je využitie vektorového súčinu, ktorého výsledkom je vektor kolmý na rovinu násobených vektorov. Preto stačí nájsť dva vektory, ktoré ležia v príslušnej rovine. Takýmito sú vektory, ktoré spájajú zadané tri body. Získame ich ako rozdiel vektorov spájajúcich  začiatok súradnicovej sústavy a zadané body. Do bodu A smeruje vektor  a = 2 i , do ďalších bodov vektory b = j ,  c = 3 k . Vektor vychádzajúci z bodu  A  a  končiaci v bode  B  je    u =  b - a  =  j  - 2 i  ,  vektor vychádzajúci  z bodu  A  a  končiaci v bode  C  je  w = c - a = 3 k -  2 i .  Potom vypočítame vektorový súčin  h =  u ´ w =  ( j  - 2 i) ´ ( 3 k -  2 i ) =  3 i  +  2 k  + 6 j .  Výsledný vektor h je kolmý na rovinu prechádzajúcu bodmi  A, B, C . Jednotkový vektor kolmý na túto rovinu získame, ak vektor  h  vydelíme jeho veľkosťou
h  = (32 + 22 + 62)1/2 = (49)1/2 = 7. 
Pre jednotkový vektor tak dostaneme:
ho =  h / 7  =  (3/7) i + (2/7) j + (6/7) k  .
 
Príklad    1.2.2.3
Vypočítajte skalárny násobok vektorového súčinu vektorov  a = 5 i ,  b = 4 i + 3 j    z  príkladu  (1.2.2.1)  skalárom  p = 2.
 
Riešenie
pc  =  p(a ´ b )  =  p[(5i) ´ (4 i + 3 j)] =  p (15 k) = 30 k .
Poznámka :  Rovnaký výsledok dostaneme, ak skalárom  p vynásobíme niektorý z vektorov  a, b  ešte pred uskutočnením vektorového súčinu :
        a)   pc =   p(a ´ b ) =  (pa ´ b) =  (10 i) ´ (4 i + 3 j) =  30 k
        b)  pc =   p(a ´ b )  =  (a ´ pb) =   (5 i)  ´ (8 i + 6 j) =  30 k
Z výsledku vyplýva významné pravidlo, že nezáleží na tom, ktorému z vektorov vektorového súčinu priradíme skalár, ktorým vektorový súčin násobíme.
 
 

Kontrolné otázky

  1. Akú veľkosť má vektor, ktorý vznikne ako vektorový súčin dvoch vektorov ?
  2. Aký smer má vektor, ktorý vznikne ako vektorový súčin dvoch vektorov ?
  3. Čo znamená, ak trojica vektorov tvorí pravotočivú sústavu ?
  4. Ako vytvoríme z pravotočivej sústavy troch vektorov ľavotočivú sústavu ?
  5. Je vektorový súčin komutatívna operácia ?
  6. Aký je geometrický význam vektorového súčinu dvoch vektorov ?
  7. Dokážete vyjadriť všetky možné kombinácie vektorových súčinov medzi vektormi  i, j, k ?
  8. Ako vyjadrujeme distributívnosť vektorového súčinu ?
  9. Viete vyjadriť vektorový súčin v tvare determinantu ?
  10. Pri násobení vektorového súčinu skalárom - možno vopred skalárom vynásobiť niektorý z vektorov súčinu, alebo až výsledný vektor ?