 Divergencia a rotácia vektorovej funkcie
Divergencia a rotácia vektorovej funkcie
Pri opise fyzikálnych polí sa často stretávame s výrazmi, ktoré možno formálne vyjadriť ako skalárny, alebo ako vektorový súčin nabla operátora s vektorovou funkciou. Označujú sa názvami divergencia, resp. rotácia vektorovej funkcie.
Divergencia vektorovej funkcie sa zavádza vzťahom:
div F(x,y,z) = Ñ × F = ( i ¶ /¶x + j ¶/¶ y + k ¶/¶z) × (Fx i + Fy j + Fz k ) =
= ¶Fx /¶x + ¶Fy /¶y + ¶Fz /¶ z (1.3.5.1)
V symbolickom skalárnom súčine nabla operátora s vektorovou funkciou sa postupuje rovnako, ako pri skalárnom súčine dvoch vektorových funkcií, zapísaných v zložkovom tvare, teda podľa vzorca (1.2.1.5). Výsledkom divergencie vektorovej funkcie je skalárna funkcia. Súčin je skutočne symbolický, lebo nabla operátor nie je v skutočnosti vektor, nemožno hovoriť o jeho veľkosti, ani o smere.
Rotácia vektorovej funkcie sa zavádza vzťahom:
rot F(x,y,z) = Ñ ´ F = ( i ¶/¶x + j ¶/¶y + k ¶/¶z) ´ (Fx i + Fy j + Fz k ) =
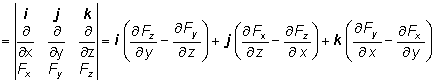 (1.3.5.2)
(1.3.5.2)Aj v tomto prípade sa symbolický vektorový súčin nabla operátora s vektorovou funkciou vykonáva podľa pravidiel vektorového súčinu medzi vektormi vyjadrenými v zložkách, teda podľa vzorcov (1.2.2.6) a (1.2.2.7) .
Príklad 1.3.5.1
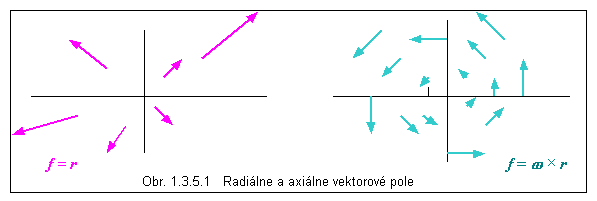
Vypočítajte divergenciu a rotáciu vektorovej funkcie f = r(x,y,z) = xi + yj + zk . Uvedomte si, že takáto funkcia (polohový vektor) má charakter radiálneho vektorového poľa, keď v ľubovoľnom bode priestoru tejto funkcii prislúcha vektor r smerujúci od stredu (začiatku) súradnicovej sústavy (obr. 1.3.5.1)
Riešenie
div r = ¶x /¶ x + ¶y /¶y + ¶z /¶z = 3
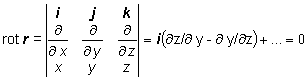
Príklad 1.3.5.2
Vypočítajte divergenciu a rotáciu vektorovej funkcie f (x,y,z) = w ´ r ktorá je vektorovým súčinom konštantného vektora w s polohovým vektorom r . Nech r = x i + y j a w = w k . Vektorová funkcia f zobrazuje pole vektora rýchlosti pri otáčaní roviny uhlovou rýchlosťou w . Je to príklad axiálneho vektorového poľa, v ktorom vektorová funkcia má vždy smer dotyčnice ku kružnici, ktorej stred leží v začiatku súradnicovej sústavy.
Riešenie
Najprv vypočítame vektorový súčin w ´ r = (w k) ´ (xi + yj) = xw j - y w i . Potom
div f = Ñ × f = Ñ × ( w ´ r ) = ( i ¶/¶x + j ¶/¶y + k ¶/¶z) × (xw j - y w i ) = 0rot f = Ñ ´ f = Ñ ´ ( w ´ r ) = ( i ¶/¶x + j ¶/¶y + k ¶/¶z) ´ (xw j - y w i ) = 2w k
Výsledky príkladov 1.3.5.1 a 1.3.5.2 hovoria o tom, že rotácia vektorovej funkcie predstavujúcej radiálne pole sa rovná nule, ale rotácia v prípade axiálneho poľa je nenulová. Naopak je to pri divergencii, kde nenulový výsledok sme dostali pri radiálnom poli. Tieto výsledky naznačujú význam operácií divergencia a rotácia pri charakterizácii fyzikálnych polí. Elektrostatické pole v okolí bodového náboja má radiálny charakter, zatiaľ čo magnetické pole v okolí vodičov elektrického prúdu charakter axiálny. Táto vlastnosť sa odzrkadľuje aj na Maxwellových rovniciach, keď pre vektor intenzity el. poľa platí div E = r/eo ale pre vektor magnetickej indukcie div B = 0 . A naopak , v elektrostatickom poli platí rot E = 0 , ale pre vektor intenzity stacionárneho magnetického poľa platí rot H = j , kde j je vektor prúdovej hustoty.
Kontrolné otázky
-
Uveďte, čo rozumieme pod divergenciou vektorovej funkcie !
-
Uveďte, čo rozumieme pod rotáciou vektorovej funkcie !
-
Napíšte rotáciu vektorovej funkcie v tvare determinatu !
-
Uveďte charakteristiky radiálneho a axiálneho vektorového poľa - aká je ich divergencia a rotácia !
