 Krivkový integrál, Stokesova veta
Krivkový integrál, Stokesova veta
Pri krivkových integráloch sa najčastešie stretávame s typom
 (1.4.2.1)
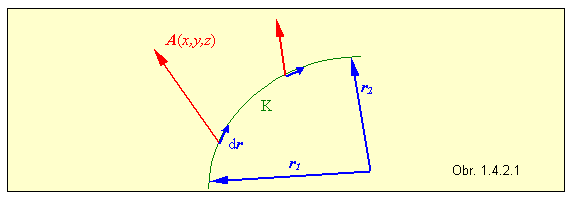
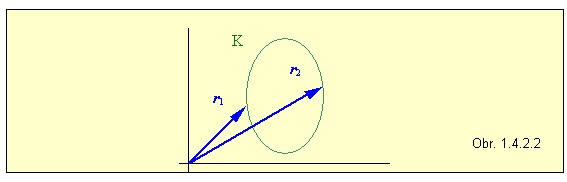
(1.4.2.1)Ide o integrál vektorovej funkcie A(x,y,z) , od začiatočného bodu r1 v zvolenej súradnicovej sústave po koncový bod určený polohovým vektorom r2 . Je to v podstate súčet limitne veľkého počtu elementárnych skalárnych súčinov A × dr = A ds cosa , kde A je veľkosť vektorovej funkcie (vektora) A , ds veľkosť príslušného dr a a uhol medzi nimi v danom bode krivky, pozdĺž ktorej integrujeme (obr.1.4.2.1). Elementárny vektor dr má v danom bode krivky K smer jej dotyčnice. Pritom veľkosť, ani smer vektora A(x,y,z) nemusia byť konštantné, od bodu k bodu na krivke sa môžu meniť.
Takýmto integrálom sa vyjadruje napríklad práca W, pričom vektorovou funkciou je sila F:
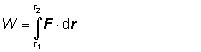 (1.4.2.2)
(1.4.2.2)Ak vektor F a diferenciál polohového vektora dr vyjadríme v zložkovom tvare, t.j.
F = Fx i + Fy j + Fz k, dr = i dx + j dy + k dz
potom po vykonaní skalárneho súčinu dostaneme
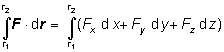 (1.4.2.3)
(1.4.2.3)takže ide o všeobecný krivkový integrál. Takýto tvar možno využiť pri praktickej realizácii výpočtu, keď chceme vypočítať číselnú hodnotu integrálu, za predpokladu, že poznáme Fx , Fy , Fz ako funkcie premenných x, y, z . Ako integračné hranice vystupujú príslušné súradnice polohových vektorov r1 a r2 . V takejto forme možno výpočet integrálu aj naprogramovať a numericky vypočítať.
Pri splnení určitých podmienok možno integrál typu (1.4.2.1) vyjadriť ako rozdiel hodnôt skalárnej funkcie v koncovom a začiatočnom bode integrácie:
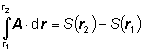 (1.4.2.4)
(1.4.2.4)To platí vtedy, ak medzi skalárnou funkciou S (x,y,z) a vektorovou funkciou A (x,y,z) platí
A = grad S , t.j.
Ax i + Ay j + Az k = (¶S /¶ x) i + (¶S /¶ y) j + (¶S /¶ z) k (1.4.2.5)
O uvedenom tvrdení sa možno presvedčiť aj pomocou vzťahov (1.3.4.2):
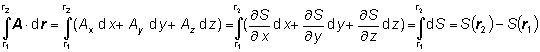
Vo vzťahoch (1.4.2.4) a (1.4.2.5) skalárna funkcia má význam potenciálu fyzikálneho poľa, vektorová funkcia význam jeho intenzity.
Príklad 1.4.2.1
Vypočítajme krivkový integrál funkcie F = 0 i + 0 j - mg k , ktorá reprezentuje homogénne tiažové pole v blízkom okolí povrchu Zeme, kde silu F považujeme za konštantnú - v každom bode priestoru má rovnakú veľkosť aj smer. Integrovať budeme od bodu A(x1, y1, z1) po bod B(x2, y2, z2) po krivke, ktorá spája tieto dva body.
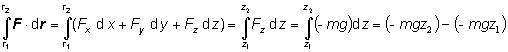
Riešenie
Podľa rovnice (1.4.2.3) platí:
Z výsledku vidno, že krivkový integrál sily F = 0 i + 0 j - mg k sa rovná rozdielu dvoch hodnôt skalárnej funkcie S (x,y,z) = -mgz , ktorá nezávisí od premenných x, y . Z výpočtu vidno, že sme nemuseli uviesť po akej krivke integrujeme, rozhodujúce sú iba začiatočný a koncový bod integrovania. Funkcia P = - S predstavuje potenciál homogénneho gravitačného poľa.
Príklad 1.4.2.2
Vypočítajme krivkový integrál funkcie F = -Kr , obmedzenej na jednu rovinu, t.j. nech napr. r = xi + yj . Ide vlastne o vyjadrenie dostredivej sily na otáčajúcom sa disku, lebo má smer opačný ako vektor r (ktorý má začiatok v strede otáčania) a čím ďalej od stredu otáčania, tým je sila väčšia. Integrovať budeme od bodu s polohovým vektorom r1 po bod r2 .
Riešenie
Funkciu F vyjadríme v zložkách F (x,y)= - K (xi + yj) , potom
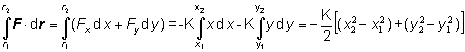
čo možno ešte upraviť na tvar zodpovedajúci rozdielu hodnôt skalárnej funkcie:
kde
(r1)2 = (x1)2 +(y1)2 , (r2)2 = (x2)2 +(y2)2.
Poznámka 1
Na príkladoch 1.4.2.1 a 1.4.2.2 sme videli, , že výsledok nezávisí od tvaru integračnej krivky, ale len od začiatočného a koncového bodu. Ak by však vo vyjadrení funkcie F bol ešte ďalší člen, ktorý by reprezentoval napríklad trenie, potom výsledok integrácie by závisel od dĺžky konkrétne zvolenej integračnej krivky. Potom by takýto integrál nebolo možné vyjadriť ako rozdiel hodnôt skalárnej funkcie v koncovom a začiatočnom bode.
Poznámka 2
Ak by sme v integráli (1.4.2.6) integrovali opačným smerom, t.j. od r2 po r1 , dostali by sme výsledok S (r1) - S (r2) , teda výsledok s opačným znamienkom. Pri integrácii po uzavretej krivke (keď začiatočný a koncový bod sú totožné) výsledok sa rovná nule, lebo na uzavretej krivke sa vyskytujú elementárne skalárne súčiny A × dr kladné i záporné v takom zastúpení, že výsledok ich súčtu je nulový. Takúto vlastnosť majú vektorové funkcie v oboch uvedených príkladoch. Prvá z nich predstavovala homogénne pole, druhá radiálne. Stretávame sa však aj s poliami, v ktorých integrál po uzavretej krivke nie je nulový, napr. v magnetickom poli, ktoré má axiálny charakter. (Pozri príklad 1.3.5.2).
Ako bolo uvedené v Poznámke 2. krivkový integrál po uzavretej krivke sa nemusí vždy rovnať nule. Vtedy obyčajne možno krivkový integrál funkcie A pozdĺž uzavretej krivky nahradiť plošným integrálom rotácie funkcie A, čo vyjadruje Stokesova veta :
Plošný integrál sa počíta cez plochu, ktorá je ohraničená integračnou krivkou K . Tvar plochy pritom nie je presne definovaný, môže to byť časť roviny, ale aj iná plocha, napríklad časť guľovej plochy, elipsoidu, či inej komplikovanejšej plochy. Pritom nie je rozhodujúce, či krivka K leží v jednej rovine. Dôkaz týchto tvrdení, vrátane dôkazu správnosti Stokesovej vety však prekračuje možnosti tohto textu. Sú predmetom matematickej analýzy.
Kontrolné otázky
-
Napíšte príklad krivkového integrálu !
-
Kedy výsledok krivkového integrálu závisí len od začiatočného a koncového bodu integrácie ?
-
Uveďte príklad krivkového integrálu, pri ktorom integrál po uzavretej krivke sa rovná nule !
-
Uveďte príklad, v ktorom výsledok krivkového integrálu závisí od integračnej cesty, a nie iba od začiatočného a koncového bodu integrácie !
-
Čo hovorí Stokesova veta ?
