Pod plošným integrálom vektorovej funkcie sa najčastejšie rozumie integrál, ktorý zapisujeme v tvare

                                                                                                      

        (1.4.3.1)

 

Za znakom dvojnásobného integrálu je skalárny súčin vektorovej funkcie A  s diferenciálom dS , ktorý ako vektor je kolmý na príslušnú elementárnu plôšku a jeho veľkosť predstavuje jej plošný obsah. Takémuto integrálu sa hovorí tok vektora A cez plochu S.

 

Aj v tomto prípade, v zmysle Riemannovej definície integrálu,  ide vlastne o súčet limitne veľkého počtu elementárnych skalárnych súčinov A × dS  = A dS cosa , kde A je veľkosť vektorovej funkcie (vektora)  A ,  dS  veľkosť príslušného dS  a  a  uhol medzi nimi v danom bode plochy, pričom sa tieto súčiny sčítajú po celej ploche, po ktorej integrujeme. Veľkosť, ani smer vektora  A(x,y,z) nemusia byť konštantné, od bodu k bodu na ploche sa môžu meniť.

 

 

 

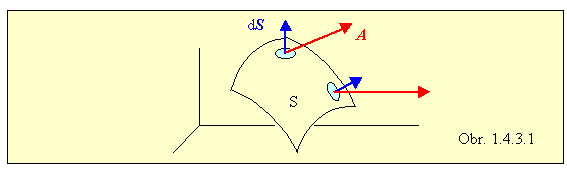
Keď dS vyjadríme v zložkách:  dS =  i dydz + j dzdx + k dxdy , skalárny súčin A × dS  možno vyjadriť aj v tvare:

 

A × dS =  A_x dydz  + A_y dzdx + A_z dxdy        (1.4.3.2)

 

takže integrál (1.4.3.1) možno vo vhodnom prípade rozpísať ako súčet troch integrálov. Výsledkom tohto integrálu je skalárna funkcia. Ako príklad možno uviesť vzťah medzi elektrickým prúdom  I   a vektorom prúdovej hustoty  j:

 

 

 

V teórii poľa sa často stretávame s plošným integrálom cez uzavretú plochu

 

        (1.4.3.3)

 

ktorý pomocou Gaussovej - Ostrogradského vety možno premeniť na objemový integrál divergencie vektorovej funkcie  A:

 

        (1.4.3.4)

 

kde  dt   predstavuje objemový element,  ktorý v  karteziánskej  súradnicovej sústave má tvar dt  =  dx dy dz . Pod uzavretou plochou pritom rozumieme napríklad povrch gule, elipsoidu, alebo iného útvaru, tvoriaceho rozhranie medzi vnútorným a vonkajším priestorom. Podľa dohody sa elementárne plošné vektory  dS  orientujú vždy z uzavretej plochy von. Správnosť tejto veľmi významnej vety na tomto mieste nebudeme dokazovať.

 

 

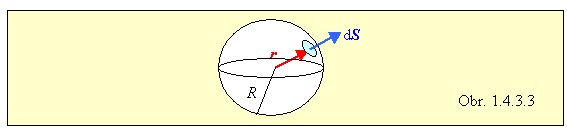
Vypočítajte plošný integrál funkcie  A = K (r /r³), kde  K  je konštanta, r polohový vektor,  r  jeho veľkosť,  cez guľovú plochu s polomerom R, ktorej stred je umiestnený do začiatku súradnicovej sústavy.

 

 

 

Pri počítaní integrálu (1.4.3.3) si uvedomíme, že vektory  r  a  dS  sú v každom bode povrchu gule rovnobežné, preto skalárny súčin  A × dS  = K (r /r³) × dS = K (1/r³) r × dS = K (1/r³) r dS =  K (1/ r²) dS, pričom na povrchu gule  r = R . Preto

 

 

lebo plošný integrál z  dS  cez celý povrch gule je  4pR² .