 Uhlová rýchlosť, uhlové zrýchlenie
Uhlová rýchlosť, uhlové zrýchlenie
Pri opise pohybov, pri ktorých polohový vektor pohybujúcej častice sa otáča, je vhodné zaviesť ďalšie významné pojmy - uhlovú rýchlosť a uhlové zrýchlenie. Býva zvykom najprv definovať veličinu uhlová dráha. Je to uhol medzi polohovými vektormi - vektorom vyznačujúcim začiatočnú polohu a vektorom v danom okamihu. Jednoduchý prípad nastane, ak sa polohový vektor otáča v jednej rovine. Na obr. 2.1.5.1 je znázornený takýto prípad.
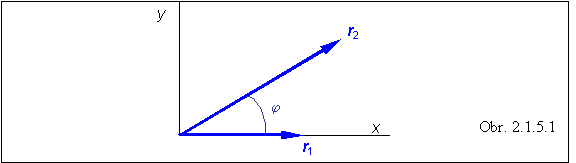
Uhol j bol vytvorený pohybom polohového vektora z polohy r 1 do polohy r2 , pričom oba vektory ležia v rovine xy . Takto vytvorenému uhlu priraďujeme vektor j , kolmý na rovinu vektorov r 1 a r2 , pričom jeho veľkosť zodpovedá veľkosti uhla. Vektor j podľa definície má taký smer, aby sa z jeho konca otáčanie vektora r 1 k vektoru r2 javilo v smere proti chodu hodinových ručičiek. ( Smeruje do tej polroviny, z ktorej vidím otáčanie prvého vektora do smeru druhého vektora po kratšej uhlovej dráhe, proti smeru hodinových ručičiek.) Na obrázku 2.1.5.1 má preto vektor j smer k čitateľovi. Uhlovú dráhu, a teda aj veľkosť príslušného vektora meriame v jednotkách radián.
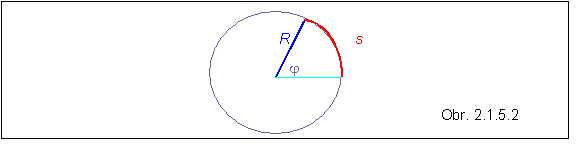
Túto jednotku možno priblížiť pomocou obrázka 2.1.5.2 , z ktorého vidno, že ak na meranie uhla používame stupne, platí úmera :
s : 2p R = j : 3600
Úmera sa zjednoduší, ak namiesto údaja 3600 dosadíme hodnotu 2p . To však znamená, že namiesto stupňov budeme na meranie uhlov používať novú jednotku radián, ktorého veľkosť vyjadrená v stupňoch je
1 rad = 3600 /2p = 57,2960
Z takto upravenej úmery dostaneme dôležitý vzťah medzi polomerom kružnice R , stredovým uhlom j a dĺžkou príslušného oblúka s na kružnici:
s = R j (2.1.5.1)
Tento vzorec pri pohybe častice po kružnici vyjadruje vzťah medzi veľkosťou dráhy prejdenej časticou po obvode kružnice a príslušnou uhlovou dráhou. Skalárne veličiny s a j závisia vtedy od času, takže:
s(t) = R j (t) (2.1.5.2)
Prvou deriváciou tohto výrazu podľa času dostaneme súvislosť
v ktorej ds/dt = v vyjadruje obvodovú rýchlosť častice (ako skalárnu veličinu) a výraz
dj /dt = w
uhlovú rýchlosť častice pri pohybe po kružnici (tiež ako skalárnu veličinu), takže:
v = R w (2.1.5.4)
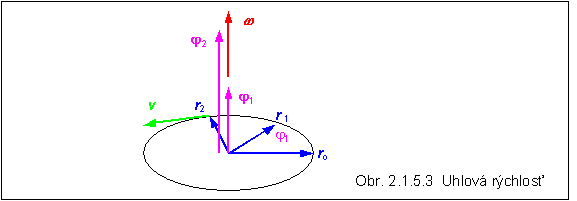
Uhlová rýchlosť w ako vektorová veličina sa zavádza podobne, ako vektor rýchlosti vzťahom:
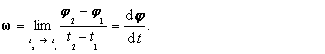 (2.1.5.5)
(2.1.5.5)Preto vektor uhlovej rýchlosti w má smer rozdielu vektorov uhlovej dráhy, ktoré sú v čitateli.
Poznámka
Pri pohybe po kružnici vektory j 1 , j 2 sú na rovinu kružnice kolmé a teda aj vektor uhlovej rýchlosti je na túto rovinu kolmý. Ak sa veľkosť vektora j s časom zväčšuje, má vektor w smer vektora j , pri jeho zmenšovaní - opačný smer.
Deriváciou rovnice (2.1.5.4) podľa času získame vzťah:
a t = R a (2.1.5.6)
kde a je (skalárne) uhlové zrýchlenie a kde at predstavuje (skalárne) tangenciálne zrýchlenie častice, pričom príslušná vektorová veličina at má smer dotyčnice kružnice určenej jednotkovým vektorom t. Celkové zrýchlenie hmotného bodu následne možno rozložiť na tangenciálnu a normálovú zložku, pre ktoré platí
a = at + an = ( a ´ r )+ (w ´ v) , (2.1.5.7)
kde a je uhlové zrýchlenie, w je uhlová rýchlosť, r je polohový vektor hmotného bodu a v obvodová rýchlosť, s ktorou sa hmotný bod pohybuje. Tangenciálna zložka zrýchlenia určuje nerovnomernosť pohybu a je určená vzťahom
at = a Rt. (2.1.5.8)
Normálová zložka zrýchlenia spôsobuje zmenu smeru a je určená vzťahom:
ktoré tiež nazývame dostredivé zrýchlenie. (r je jednotkový vektor so začiatkom v strede kružnice S. ) Veľkosť celkového zrýchlenia hmotného bodu je určená vzťahom
Uhlové zrýchlenie a ako vektorová veličina sa definuje vzťahom
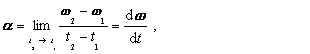 (2.1.5.11)
(2.1.5.11)a pri pohybe po kružnici je na jej rovinu kolmé. O jeho smere platí podobná poznámka, ako o smere vektora uhlovej rýchlosti.
Príklad 2.1.5.1
Hmotný bod sa začal pohybovať po kružnici polomeru r s konštantným uhlovým zrýchlením a . V ktorom časovom okamihu bude vektor zrýchlenia zvierať uhol b = 60 0 s vektorom rýchlosti v?
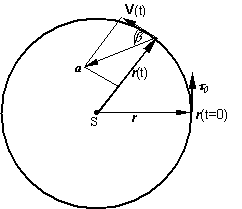
Riešenie
Kým začneme riešiť je vhodné si uvedomiť skutočnosti:
-
Jedná sa o rovnomerne zrýchlený pohyb po kružnici so začiatočnými podmienkami j0 = 0 a w 0 = 0.
-
Vektor rýchlosti v má smer dotyčnice ku trajektórii pohybu.
-
Vektor zrýchlenia rozložíme na tangenciálnu a normálovú zložku.
-
Vektor rýchlosti je kolineárny (rovnobežný) s tangenciálnou zložkou zrýchlenia.
-
Uhol b, ktorý zviera vektor zrýchlenia s vektorom rýchlosti je aj uhol, ktorý zviera vektor zrýchlenia s vektorom tangenciálnej zložky zrýchlenie, pre ktorý platí:
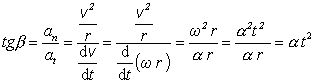
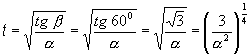
Kontrolné otázky
-
Charakterizujte krivočiary pohyb.
-
Uveďte niektoré špeciálne prípady krivočiareho pohybu.
-
Aký smer má rýchlosť pri krivočiarom pohybe?
-
Do akých zložiek rozkladáme vektor zrýchlenia pri krivočiarom pohybe v rovine?
-
Ak sa teleso pohybuje s konštantným celkovým zrýchlením rozhodnite, či môže mať jeho dráha tvar určenú ktoroukoľvek z nasledovných kriviek: a) priamka b) kružnica c) špirála d) ľubovolný tvar.
-
Môže byť vektor rýchlosti konštantný pri krivočiarom pohybe?
-
Ak častica koná rovnomerný krivočiary pohyb, aký smer má vektor rýchlosti?
-
Vyjadrite dĺžku ubehnutej dráhy hmotného bodu, ktorý sa pohybuje krivočiarym pohybom a) v rovine, b) v priestore
-
Akým smerom je orientovaný vektor okamžitej rýchlosti vzhľadom na trajektóriu?

