Pohyb častice po kružniciPohyb častice po kružnici

Pri opise pohybu po kružnici sa s výhodou používajú skalárne veličiny zavedené v časti 2.1.5 . Sú to  : uhlová dráha   s  (s = Rj  (2.1.5.1)) ,  obvodová rýchlosť    (v = Rw  (2.1.5.4))  a  tangenciálne zrýchlenie  a t  (a t  =  Ra  (2.1.5.6)).
 
Ďalšou významnou veličinou je doba obehu (perióda) označovaná symbolom  T , predstavujúca časový interval potrebný na jeden obeh po kružnici. Prevrátená hodnota doby obehu je  frekvencia:   f = (1/ T) . Jednotkou frekvencie je  1 herz  (Hz). (Pozri príklad 2.1.8.1).
 
 
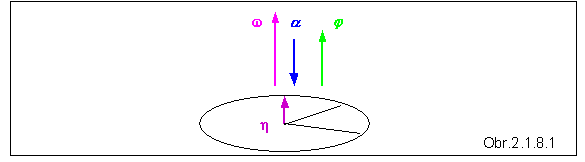
Pri pohybe častice po kružnici podrobnejšie opíšeme pohyb s konštantnou uhlovou rýchlosťou a  pohyb s konštantným uhlovým zrýchlením. Zvolíme  jednotkový vektor h kolmý na rovinu kružnice. Na túto rovinu sú kolmé aj vektory uhlovej dráhy  j , uhlovej rýchlosti w  a uhlového zrýchlenia  a  , takže ich môžeme vyjadriť ako skalárne násobky vektora h  :  
 
j  =  j hh  ,      w  =  wh h ,      a  = ah h ,        (2.1.8.1)          
                                              
kde skalárne veličiny  jh  ,  wh    a ah   predstavujú súradnice príslušných vektorových veličín, nie ich veľkosti , takže môžu byť aj záporné. Napr. na obr. 2.1.8.1  má vektor a  opačný smer ako jednotkový vektor  h , takže  súradnica uhlového zrýchlenia  ah    musí  byť záporná.
 
Poznámka
Veľkosti uhlovej dráhy, uhlovej rýchlosti a uhlového zrýchlenia, ktoré nemôžu byť záporné, budeme označovať bez indexu vyjadrujúceho vzťah k jednotkovému vektoru, teda ako j , w , a  .
 
Pohyb s nemeniacou sa uhlovou rýchlosťou sa označuje ako rovnomerný pohyb po kružnici. Podľa definície uhlovej rýchlosti  (2.1.5.5) platí  dj  =  w dt  a  integráciou tohto vzťahu dostaneme:   
 
  
                                              
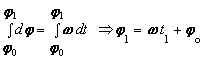
Vynechaním indexu "jeden"  dostaneme vzorec platný v ľubovoľnom okamihu  t .
                                              
 j  =  w t  +  j o .        (2.1.8.2)
 
V tomto vzorci sú všetky vektory kolineárne s jednotkovým vektorom h , ktorým vzorec skalárne vynásobíme :
 
(j  ×  h )  =  (w .  h ) t  + (jo × h  )  Þ    (jh h . h ) =  (w h h . h )t +  (jho h .h ) ,
 
čo dáva výsledok
                                                          
jh  =  w h t  + j ho.        (2.1.8.3)
 
Pokiaľ by sme vo vzťahu (2.1.8.3) nepísali indexy, takže by išlo o veľkosti (absolútne hodnoty) veličín, museli by sme zvažovať, či príslušné vektory majú rovnaký, alebo opačný smer ako jednotkový vektor  h  . Ak by napríklad vektor  w   mal opačný smer ako vektor h ,  ich skalárny súčin by bol záporný, takže vzorec (2.1.8.3) by sme museli písať aj so znamienkom (pozri príklad 2.1.4.1):
                                                          
j  =  - w t  + j o.        (2.1.8.4)
 
Pri pohybe konštantnou uhlovou rýchlosťou je uhlové zrýchlenie nulové a preto nulové je aj tangenciálne zrýchlenie (pozri vzťahy 2.1.5.6).
 
 
Príklad  2.1.8.1  
Nájdite vzťah medzi dobou obehu (periódou) a uhlovou rýchlosťou pri rovnomernom pohybe po kružnici.
 
Riešenie
Pre rovnomerný pohyb po kružnici platí vzorec   j  -  j o  =  w t  .  Pri jednom obehu častica prejde uhlovú dráhu  2p  radiánov,  pričom uplynie čas rovnajúci sa dobe obehu  T . Preto platí  2p  = wT , alebo 
 
w = 2p /T  =  2p f ,        (2.1.8.5)
 
kde  f  je frekvencia pohybu po kružnici.
 
 
Ďalším významným prípadom je pohyb s konštantným uhlovým zrýchlením, teda rovnomerne zrýchlený pohyb  po kružnici. Podľa definície uhlového zrýchlenia  (2.1.5.11)  platí  dw  =  a  dt .  Integráciou tohto vzťahu dostaneme závislosť uhlovej rýchlosti od času :  
                       
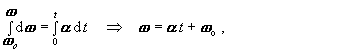(2.1.8.6)
 
kde  w o  je uhlová rýchlosť v čase  t = 0. 
Keďže  dj  =  w dt, závislosť uhlovej dráhy od času pri rovnomerne zrýchlenom pohybe získame ďalšou integráciou:
 
 
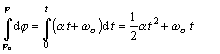
a po úprave
 
        (2.1.8.7)
 
 
Pre skalárny tvar rovníc   (2.1.8.6)  a  (2.1.8.7)   platia rovnaké poznámky, ako pri rovniciach (2.1.8.1)  a (2.1.8.4). Pri rovnomerne zrýchlenom pohybe po kružnici sa tangenciálne zrýchlenie  a t = R a  nemení . Mení sa uhlová rýchlosť, takže sa mení aj dostredivé zrýchlenie, pre ktoré potom platí  ad = R w 2 = R (ah t  + w o )2. Dostredivé a tangenciálne zrýchlenie sú na seba kolmé, preto veľkosť celkového zrýchlenia vypočítame využitím Pythagorovej vety: 
 
    
 
Príklad  2.1.8.2 
Na valcové jadro, ktoré má polomer r = 3 cm, chceme v jednej vrstve navinúť n = 600 závitov tenkého drôtu. a) Koľko metrov drôtu potrebujeme? b) Akou uhlovou rýchlosťou w  sa musí pri navíjaní valec otáčať, aby sme drôt navinuli za Dt = 5 minút ? c) Aká musí byť pritom frekvencia f  otáčania valca ?
 
Riešenie 
a) Dĺžka drôtu  d = n . 2p r  =  600 . 6,28 . 0,03 m = 113 m
b) Navinúť  n  závitov znamená otočiť valec o uhol  j  = n . 2p radiánov . Potom použijeme vzťah (2.1.8.2) ,  j = w t  + j o , v ktorom položíme  j o = 0 a dosadíme vypočítanú hodnotu j  = n . 2p  a požadovanú dobu navíjania  Dt  :   w  =  j / Dt   =  n . 2p / Dt   = 600 . 2p rad / 300 s  =  12,57 rad/s .
c) Medzi uhlovou rýchlosťou a frekvenciou platí vzťah (2.1.8.5), z ktorého vypočítame  f = w / 2p  , čo číselne poskytuje   f  =  2 Hz .  Valec sa musí otočiť dvakrát za sekundu.
 
Príklad  2.1.8.3
Na cievku s polomerom r = 5 cm , ktorá sa otáčala frekvenciou  fo = 90 otáčok za minútu, sa navíjal drôt. Po vypnutí pohonu (v okamihu to = 0 s) sa cievka ešte otáčala rovnomerne spomaleným pohybom a zastavila sa v čase  t2 = 3 s.
                a) Aká bola začiatočná uhlová rýchlosť cievky w o  ?
                b) Aké bolo pritom uhlové zrýchlenie a  (vlastne spomalenie) cievky ?
                c) Koľkokrát sa po vypnutí pohonu cievka ešte otočila ?
                d) Aká dĺžka drôtu  d  sa na cievku navinula po vypnutí pohonu ?
                e) Aké bolo tangenciálne zrýchlenie drôtu at  po vypnutí pohonu ?
 
Riešenie 
a)  
 
fo  =  90 / (60 s) = 1,5 s-1 = 1,5 Hz  ,  Þ    w o = 2p fo  =  3p  rad/s
 
b)
Využijeme skalárny tvar rovnice (2.1.8.4 ) :   w  =  - a t + w o  . Záporné znamienko pri prvom člene na pravej strane je dôsledkom spomaľovania otáčania. Pri takomto zápise značka  a predstavuje absolútnu hodnotu (= veľkosť) uhlového "zrýchlenia" . V okamihu  t2  sa cievka zastavila, takže  w  = 0 , čo využijeme na výpočet   a:  
 
0 = - at2  + w o     Þ     a  = w o / t2  =  (3p  rad/s) / 3 s  =   p  rad/s2
 
c)
Použijeme upravený skalárny tvar vzorca (2.1.4.1) :  j  =  - (1/2) a t 2  + w o t  , v ktorom sme zvolili  j o = 0  . Keď dosadíme  t = t2  , dostaneme uhol 
 
j 2  =  w o t2  - (1/2)a t22  =  (3p  rad/s . 3 s)  -  (0,5.p  rad/s2 . 3 s2 ) = 7,5 p  rad
 
Počet otočení dostaneme, ak uhol otočenia  j 2  vyjadrený v radiánoch,  vydelíme počtom radiánov pripadajúcich na jedno otočenie:  
 
n  =  (7,5 p  rad) / ( 2p  rad) = 3,25
 
d)
Dĺžku navinutého drôtu vypočítame vynásobením obvodu cievky počtom otočení: 
 
d  = n . 2p r  =  3,25 . 6,28 . 0,05 m  =  1,02 m
 
e)
Tangenciálne zrýchlenie vypočítame podľa vzťahu 2.1.5.5: 
 
at  =  R a  = 0,05 m . p  rad/s2 =  1,57 m/s2
 
Poznámka
Jednotka uhla  rad  je bezrozmerná, preto sa vo výsledku pre   at   neuvádza.
 
 
Príklad  2.1.8.4
Častica sa pohybuje po kružnici s uhlovým spomalením, ktoré s časom rovnomerne rastie podľa vzťahu a = kt, kde k je konštanta a t je čas. Začiatočná uhlová rýchlosť bola w0. O aký uhol j sa pootočí sprievodič častice za čas  t1?
 
Riešenie
Uhlového zrýchlenie a je definované vzťahom (2.1.5.11),  do ktorého dosadíme časovú závislosť uhlového zrýchlenia , vyjadrenú vzťahom   -a = k t
 
 
Integračnú konštantu určíme z počiatočných podmienok:   pre t = 0,  c = w0 . Hľadaná uhlová rýchlosť je určená vzťahom
 
w =w0 – kt2 / 2.
 
Uhol, o ktorý sa pootočí sprievodič za čas t1 určíme na základe úpravy rovnice  (2.1.5.5 )
 
 
 
 
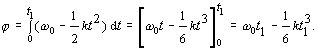
Príklad  2.1.8.5
Bod sa pohybuje po kružnici polomeru R tak, že ním prebehnutá dráha je daná vzťahom
 
 
kde vo a k sú konštanty. Aká je absolútna hodnota celkového zrýchlenia? V ktorom časovom okamihu  tk  sa táto hodnota stane rovnou k? Koľko obehov  urobí bod do tohto okamihu?
 
Riešenie
Vyjadríme si  rýchlosť, tangenciálne a dostredivé zrýchlenie pre danú časovú závislosť dráhy vzťahmi:
 
 
 
 
 
Určime časový okamih tk , kedy celkové zrýchlenie je rovné konštante k, t.j. platí
 
 
Umocnením rovnice a úpravou získame hľadaný časový okamih
 
 
Pre tangenciálne zrýchlenie,  určené vzťahom  (2.1.7.7) po dosadení za deriváciu dostávame
 
at = aR = -k  Þa = -k/R.
 
Úpravou a dosadením do rovnice (2.1.5.11) pre uhlovú  rýchlosť dostávame
                       
 
 
Integračnú konštantu určíme z počiatočných podmienok:  v okamihu
 

t = 0   w = wo = v0 (t)R = voR  Þ     c= v0 /R 

 
Na základe vzťahu (2.1.5.5) pre uhlovú dráhu dostávame

 
Integračná konštanta C, určená  z podmienok: t = 0 ,   j = 0 , je rovná nule. Pre  uhlovú dráhu platí
 
 
Počet otáčok za časový interval tk  určuje vzťah
 
 
 

Kontrolné otázky

  1. Charakterizujte otáčavý pohyb.
  2. Definujte a) rovnomerný, b) nerovnomerný pohyb po kružnici.
  3. Vysvetlite   fyzikálny význam   uhlovej rýchlosti w.
  4. Ak sa častica pohybuje rovnomerným pohybom po kružnici, je nenulové jej zrýchlenie?
  5. Napíšte a definujte, ktoré veličiny charakterizujú pohyb po kružnici.
  6. Napíšte jednotku uhlovej rýchlosti a uhlového zrýchlenia.
  7. Pod vplyvom pôsobenia akej fyzikálnej veličiny sa mení priamočiary pohyb na pohyb po kružnici?
  8. Napíšte vzťah pre obvodovú rýchlosť častice pohybujúcej sa rovnomerným pohybom po kružnici s polomerom r a s uhlovou rýchlosťou w.
  9. Napíšte súvis periódy  T s frekvenciou  f  pri rovnomernom pohybe po kružnici.
  10. Napíšte súvis medzi periódou   T a uhlovou rýchlosťou pri rovnomernom pohybe po kružnici.
  11. S akou uhlovou rýchlosťou sa pohybuje a) sekundová, b) minútová, c) hodinová ručička na hodinách?
  12. Je vektor rýchlosti konštantný pri rovnomernom pohybe po kružnici?
  13. Je vektor zrýchlenia konštantný pri rovnomernom pohybe po kružnici?
  14. Definujte vektor uhlového zrýchlenia a napíšte jeho jednotku.
  15. Akú  vzájomnú orientáciu majú vektory uhlovej rýchlosti, polohového vektora častice a  jeho obvodovej rýchlosti pri pohybe častice po kružnici?
  16. Určite smer dostredivého zrýchlenie pri pohybe po kružnici.
  17. Napíšte matematické vyjadrenie pre tangenciálne  zrýchlenie pri pohybe po kružnici.
  18. Napíšte vzťah pre celkové zrýchlenie pri pohybe po kružnici.
  19. Určite ako sa zmení obvodová rýchlosť častice pohybujúcej sa konštantnou uhlovou rýchlosťou po kružnici, ak jej vzdialenosť od osi rotácie zmenšíme na polovicu?
  20. Teleso sa pohybuje s normálovým zrýchlením rovným nule. Aká môže byť jeho  dráha v tomto prípade?
  21. Nakreslite grafickú závislosť  veľkosti uhlového zrýchlenia hmotného bodu ako funkciu času, ak sa hmotný bod  pohybuje po kružnici:      a) rovnomerne , b) rovnomerne zrýchlene.
  22. Nakreslite grafickú závislosť veľkosti uhlovej dráhy  ako funkciu času, ak sa hmotný bod  pohybuje po kružnici: a) rovnomerne , b) rovnomerne zrýchlene. Zvoľte si najjednoduchšie počiatočné podmienky.
  23. Aký pohyb koná hmotný bod , ak celkové zrýchlenie sa rovná tangenciálnemu zrýchleniu? Zložka  tangenciálneho zrýchlenia klesá s druhou mocninou času.
  24. Ak sa teleso  pohybuje s  konštantným celkovým zrýchlením rozhodnite, či môže mať   jeho dráha tvar určenú ktoroukoľvek z nasledovných kriviek : a) priamka     b) kružnica    c) špirála    d)  ľubovolný tvar.
  25. Môže byť vektor rýchlosti konštantný pri krivočiarom pohybe?
  26. Napíšte matematické vzťahy, vyjadrujúce súvislosť medzi uhlovou dráhou, uhlovou rýchlosťou a uhlovým zrýchlením.