 Pohyb častice po krivke
Pohyb častice po krivke
V paragrafoch 2.1.4 a 2.1.8 boli opísané pohyby častice po priamke a po kružnici. Sú to špeciálne prípady pohybu. Pohyb po zložitejších čiarach možno na niektorých ich krátkych úsekoch aproximovať pohybom po priamke, alebo pohybom po kružnici. Častejšie je však zvykom takéto pohyby opisovať pomocou zmien súradníc polohového vektora, a súradníc vektora rýchlosti - v trojrozmernom priestore pomocou troch súradníc, pri pohybe v rovine pomocou dvoch súradníc.
Krivočiary pohyb je charakterizovaný tým, že trajektória, ktorú opisuje hmotný bod je ľubovolná krivka. Ak časová závislosť polohového vektora sa mení podľa rovnice
r = r (x, y, z, t), (2.1.9.1)
hovoríme o pohybe v priestore. V tomto prípade musíme vychádzať z vektorovej rovnic r = f(t), resp. z troch skalárnych rovníc
x = f1(t), y = f2(t), z = f3(t), (2.1.9.2)
kde parametrom je premenná čas t. Tvar krivky, po ktorej sa pohybuje hmotný bod, určený parametrickými rovnicami (2.1.9.2), určíme vylúčením parametra t, čím získame všeobecnú rovnicu dráhy.
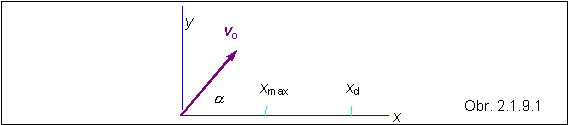
Najjednoduchším a najznámejším príkladom, ktorý sa takto opisuje, je šikmý vrh . Ak hodíme kameň, ktorý možno v istom priblížení považovať za hmotný bod, pohybuje sa približne po parabolickej dráhe (považujeme ho za dostatočne malý a tak neuvažujeme jeho rotáciu okolo osi prechádzajúcej jeho ťažiskom). Vo vákuu v zemskom tiažovom poli by sa pohyboval po skutočnej parabole. Takýto prípad, keď neuvažujeme odpor prostredia, sa opisuje pomocou pohybu vo vertikálnej rovine. Vo vodorovnom smere v rovine zvolíme súradnicu x a jednotkový vektor i , vo zvislom smere zvolíme súradnicu y a jednotkový vektor j . Pohybu častice (kameňa) vo vodorovnom smere nebráni odpor prostredia, ani iná sila, preto si zachováva príslušnú zložku rýchlosti vx = vxo , ktorou bola hodená. Pohyb v smere osi x je teda pohybom s nemeniacou sa rýchlosťou - pohyb rovnomerný. Vo zvislom smere podlieha častica tiažovému zrýchleniu, takže v smere osi y ide o pohyb s konštantným zrýchlením, čiže o pohyb rovnomerne zrýchlený. Pohyb po parabolickej dráhe v tomto prípade opíšeme pomocou dvoch priamočiarych pohybov, s využitím rovníc (2.1.4.4), (2.1.4.9) a (2.1.4.11) . Kameň hodíme začiatočnou rýchlosťou vo tak, že s vodorovnou osou zviera uhol a . Potom platia vzťahy
vxo = vo cos a , vyo = vo sin a
Preto môžeme napísať rovnice :
x (t) = xo + vx t vx = vxo ax = 0
y (t) = yo + vyo t - (1/2)g t2 vy = vyo - gt ay = -g
ktoré úplne popisujú šikmý vrh. Ich pomocou možno vypočítať napríklad závislosť miesta dopadu (na osi x) od začiatočnej rýchlosti a uhla a , časový interval od okamihu hodu až po dopad, súradnice najvyššieho bodu dráhy, alebo počítať uhol, pri ktorom zaletí kameň najďalej. Rovnice sa zjednodušia, keď predpokladáme, že xo a yo sa rovnajú nule.
V najvyššom bode dráhy platí vy = 0 , čo sa splní v časovom okamihu t1 , takže platí
vyo - gt1 = 0 Þ t1 = (vo sin a ) /g
Tento vypočítaný čas dosadíme do rovnice pre súradnicu y, čím získame najvyššiu polohu dráhy :
ymax = vo t1 sin a - (1/2)g t1 2 = (vo2 sin2 a ) /(2g)
Vodorovnú súradnicu najvyššieho bodu získame, ak čas t1 dosadíme do vzorca pre x :
xmax = vx t1 = (vo cos a )( vo sin a ) /g = (vo2 sin 2a) / 2g
Okamih t2 dopadu na os x získame z podmienky
yd = 0 Þ vo t2 sin a - (1/2)g t2 2 = 0 Þ t2 = 2(vo sin a ) /g
Vidno, že platí t2 = 2 t1 . Dosadením do rovnice pre súradnicu x dostaneme zrejme
xd = 2 xmax = (vo2 sin 2a) / g
Z posledného výsledku bezprostredne vidno, že pri istej začiatočnej rýchlosti vo kameňom najďalej dohodíme pri sin 2a = 1 , teda pri a = p/4 . Takýto výsledok však platí iba vo vákuu, pri reálnych podmienkach, keď treba vziať do úvahy odpor prostredia, je potrebný uhol o niečo menší ako p/4 .
Že ide v tomto prípade o pohyb po parabole sa presvedčíme, keď spojíme rovnice pre x(t) a y(t) tak, že vylúčime z nich čas, ktorý možno chápať ako parameter. Tak dostaneme :
y = x (sin a / cos a) - x2 g /(2 vo2 cos2 a)
čo je rovnica paraboly.
Podobným spôsobom možno opísať aj pohyb po kružnici. Treba vhodne vyjadriť x-ovú a y-ovú súradnicu častice pohybujúcej sa po kružnici, ako funkcie času :
x (t) = R sin (w t) y(t) = R cos (w t)
Že ide o pohyb po kružnici, si možno overiť tak, že obe rovnice umocníme na druhú a sčítame :
x2 (t) + y2 (t) = R 2
čo je rovnica kružnice. Nejde však o pohyb po súradnicových osiach s konštantnou rýchlosťou, či konštantným zrýchlením. Rýchlosť získame deriváciou príslušných súradníc podľa času:
vx = Rw cos (w t) vy = - Rw sin (w t) Þ
v = (vx2 + vy2)1/2 = Rw
čo opäť naznačuje, že ide o pohyb po kružnici s polomerom R uhlovou rýchlosťou w . Druhou deriváciou získame súradnice zrýchlenia, a pre jeho veľkosť vyjde Rw2 , teda hodnota dostredivého zrýchlenia.
Podobným spôsobom možno opísať pohyb častice po iných krivkách, napr. elipse, hyperbole, ale aj zložitejších krivkách. Pohyb v priestore si bližšie ozrejmíme na konkrétnych príkladoch.
Príklad: 2.1.9.1
Časová závislosť pohybu hmotného bodu je určená parametrickými rovnicami x = k1, y = k2t + k3t3, kde k1, k2 a k3 sú konštanty. Rozhodnite, aký pohyb koná hmotný bod a určite rýchlosť a zrýchlenie hmotného bodu v základných jednotkách sústavy SI a) na konci tretej sekundy pohybu, b) na začiatku jedenástej sekundy pohybu, ak k1 = 3 mm, k2 = 10 cm.s-1, k3 = 500 mm.s-3.
Riešenie
Zadané veličiny vypíšeme a ak nie sú v základných jednotkách SI sústavy premeníme ich:
k1 = 3 mm = 3.10-3 mk2 = 10 cm. s-1 =10. 10-2 m.s-1 = 10-1 m.s-1k3 = 500 mm.s-3 = 500.10-6 m.s-3 = 5.10-4 m.s-3a) t1 = 3 s, v1 = ? , a1 = ?b) t2 = 10 s, v 2 = ? , a 2 = ?
Pohyb hmotného bodu je daný dvoma rovnicami pre časovú závislosť polohového vektora r(t) = [x (t), y(t) ] = [x, y], takže sa jedná o pohyb v rovine xy. Rýchlosť a zrýchlenie sú vektorové fyzikálne veličiny, musíme určiť aj ich veľkosť aj ich smer. Napíšeme si základné vzťahy pre hľadané veličiny v = [ v x, v y ] a a = [ax, ay ], kde
Smer vektorov v a a určíme z trigonometrickej funkcie cos a.
Do základných vzťahov dosadíme zadané parametrické rovnice a vykonáme naznačené matematické operácie:
Pre veľkosť a smer rýchlosti po číselnom dosadení dostávame v prípade:
a) v(t1) = 10-1 m.s-1 + 3. 5.10-4 m.s-3(3 s)2 = ( 0,1 +0,0135) m.s-1 = 0,1135 m.s-1
Poznámka
Pre určenie smeru možno zvoliť i inú trigonometrickú funkciu. Ak by sme si zvolili
vidíme, že funkcia nie je definovaná, nakoľko x-ová zložka rýchlosti je nulová. Vieme teda, že pohyb hmotného bodu sa uskutočňuje v smere odklonu od x-ovej osi určenom uhlom a = 90 o, čo odpovedá smeru osi y .
b) v (t2) = 10-1 m.s-1 + 3. 5.10-4 m.s-3(10 s)2 = ( 0,1 +0,15) m.s-1 = 0,25 m.s-1.
Pre zadaný prípad, obdobne smer vektora rýchlosti je v smere osi y. Zrýchlenie určíme na základe už uvedených vzťahov
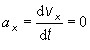 ,
, 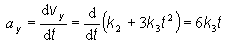 ,
, Pre veľkosť a smer zrýchlenia , po číselnom dosadení, dostávame v prípade
a) a (t1) = 6 k3 t1 = 6. 5.10-4 m.s-3(3 s) = 0,009 m.s-2
a (t1) = 0,009 j [m.s-2] .
b)
a (t2) = 0,3 j [m.s-2 ]
čo znamená, že aj vektor rýchlosti a leží v smere súradnicovej osi y .
Odpoveď
Hmotný bod pohybujúci sa podľa parametrických rovníc v zadaní vykonáva nerovnomerný priamočiary pohyb v smere jednotkového vektora j s veľkosťou rýchlosti v = 0,235 m.s-1 a veľkosťou zrýchlenia a = 0,09 m.s-2 na konci tretej minúty, resp. v = 2,5 m.s-1 a a = 0,3 m.s-2 na začiatku jedenástej sekundy.
Príklad 2.1.9.2
Mucha lieta tak, že jej súradnice závisia od času podľa rovníc: x = R sin w t , y = A t, z = R cos w t, kde R, w a A sú konštanty. Rozhodnite, o aký pohyb sa jedná a určite vektor rýchlosti a vektor zrýchlenia jej pohybu, ako i veľkosť zložky tangenciálneho a normálového zrýchlenia.
Riešenie
Zo zadania troch parametrických rovníc vieme povedať, že mucha vykonáva priestorový pohyb. Dráha je skrutkovnica v smere osi y, určená parametrickými rovnicami
x = R sin w t
y = At
z = R cos w t
Vektor rýchlosti určíme zo vzťahu
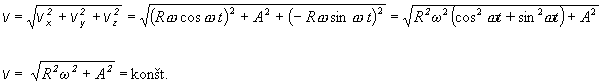
Vektor zrýchlenia určíme ako deriváciu vektora rýchlosti
Príklad 2.1.9.3
Zrnko prachu sa pohybuje po skrutkovnici tak, že jeho polohový vektor r v čase t je určený rovnicou : r = iR cos w t +jR sinw t + k v t , kde R, w a v sú kladné konštanty. Akú dlhú dráhu s prejde zrnko za časový interval Dt = t – t0 , keď v čase t0 = 0 sa nachádzalo zrnko v začiatku súradnicového systému, t.j. r0 = 0.
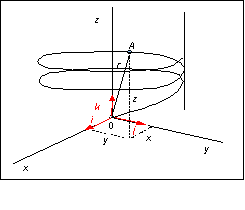
Riešenie
Elementárna dĺžka dráhy ds, ktorú zrnko prebehne je daná rovnicou
pričom z rovníc: x = R cos w t, y = R sin w t, z = n t pre jednotlivé diferenciály platí:
dx = -R w sin w t dt, dy = Rw cos w t dt, dz = v dt. (2)
Po dosadení vzťahov (2) do rovnice (1) dostaneme:
Integrovaním rovnice (3) dostaneme celkovú dĺžku dráhy Ds , ktorú zrnko prešlo za časový interval D t = t
Kontrolné otázky
-
Charakterizujte krivočiary pohyb.
-
Napíšte parametrické rovnice vyjadrujúce pohyb v priestore.
-
Napíšte parametrické rovnice vyjadrujúce pohyb v rovine.
-
Uveďte niektoré špeciálne prípady krivočiareho pohybu.
-
Aký smer má rýchlosť pri krivočiarom pohybe?
-
Do akých zložiek rozkladáme vektor zrýchlenia pri krivočiarom pohybe v rovine?
-
Vyjadrite dĺžku ubehnutej dráhy hmotného bodu, ktorý sa pohybuje krivočiarym pohybom a) v rovine, b) v priestore.
-
Ovplyvňujú sa navzájom jednotlivé zložky popisujúce priestorový pohyb?
-
Môže sa častica pohybovať po špirále, ak jej normálové zrýchlenie je nulové?
-
Ak častica koná rovnomerný krivočiary pohyb, aký smer má vektor rýchlosti?
-
Napíšte matematické vyjadrenie veľkosti rýchlosti a dráhy voľne padajúceho telesa.
-
Je niektorá zložka vektora rýchlosti konštantná pri šikmom vrhu v homogénnom gravitačnom poli?
-
Aká je rýchlosť telesa vrhnutého zvisle nahor v najvyššom bode jeho dráhy?
-
Aký uhol zviera vektor rýchlosti častice konajúcej šikmý vrh v najvyššom bode jej dráhy s osou nezávisle premennej, ktorou je čas t?
-
Možno použiť rovnice paraboly v parametrickom tvare pre opis šikmého vrhu?
-
Napíšte parametrické rovnice pre rýchlosť i dráhu, hmotného bodu konajúci šikmý vrh.

