Impulz sily a hybnosť častice, moment hybnosti a moment silyImpulz sily a hybnosť častice, moment hybnosti a moment sily

Impulz sily a hybnosť častice
Pod impulzom sily rozumieme časový účinok sily, zjednodušene povedané súčin pôsobiacej sily a časového intervalu jej pôsobenia. Presnejšie by sme mali hovoriť o skalárnom násobku vektora sily f  časovým intervalom D t:
 
I = f Dt        (2.2.3.1)
 
Ak nie je časový interval veľmi krátky, sila sa môže počas intervalu badateľne zmeniť. Preto celkom všeobecná definícia impulzu sily ako vektorovej veličiny  má tvar :
 
(2.2.3.2)
 
kde  t1  a  t2  predstavujú začiatok a koniec časového intervalu pôsobenia sily.
Impulz sily pôsobiaci na voľnú časticu (hmotný bod) s hmotnosťou  m  vyvolá zmenu jej rýchlosti, lebo pri pôsobení sily f, častica sa pohybuje zrýchlením  a. Namiesto sily  f  môžeme do vzorca (2.2.3.2)  dosadiť súčin  ma  a integrál upraviť :
 
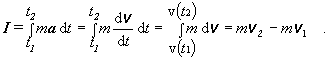        (2.2.3.3)
 
Súčin  p =  mv  hmotnosti  m  častice a jej rýchlosti  v  nazývame  hybnosť častice (hmotného bodu). Hybnosť je vektorová veličina a v našej fyzikálnej literatúre sa často označuje písmenom  H . Z predošlého vzorca vyplýva, že impulz sily pôsobiaci na časticu má za následok zmenu jej hybnosti - z hybnosti  m v 1  v časovom okamihu  t1  na  hybnosť  m v 2  v okamihu  t2 . Rovnica (2.2.3.3) je vektorová, to znamená, že impulz sily môže meniť veľkosť, ale aj smer vektora hybnosti častice.
 
Jednotkou impulzu  sily, ale aj hybnosti  v SI je  N.s (newton sekunda). V prípade ak pôsobiaca sila nie je konštantná a nepoznáme jej časový priebeh,  ale  poznáme počiatočnú a konečnú hodnotu hybnosti hmotného bodu, môžeme určiť strednú hodnotu silu pôsobiacej na hmotný bod počas časového intervalu Dt  vzťahom.
 
fs   = (p2  -p1 )/Dt 
                                                                                                       
Rovnicu (2.2.3.3) možno upraviť z integrálneho do diferenciálneho tvaru. Pre elementárny impulz platí  
                          
dI  =  f dt  =  ma dt  =  m (dv / dt) dt  =  m dv  =  d (mv) = dp,
 
odkiaľ získame vzťah
 
f  =  (dp / dt),        (2.2.3.4)
 
čiže:
sila pôsobiaca na časticu sa rovná derivácii jej hybnosti podľa času.
 
Rovnicav tvare  (2.2.3.4) vyjadruje druhý  Newtonov pohybový zákon. Po úprave a  integrovaní  rovnice  (2.2.3.4) dostaneme       
 
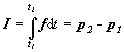        (2.2.3.5)            
 
ktorý možno slovne vysloviť: Impulz sily pôsobiacej na voľný hmotný bod sa rovná zmene hybnosti hmotného bodu. Rovnicu (2.2.3.5) nazývame tiež  prvá veta impulzová pre hmotný bod.
 
 
Príklad  2.2.3.1
Lopta s hmotnosťou  m = 0,2 kg  narazila na stenu pod uhlom dopadu  60o  a odrazila sa pod rovnakým uhlom, pričom veľkosť jej rýchlosti sa nezmenila. Určite strednú silu fstr   pôsobiacu na loptu počas nárazu, ktorý trval  Dt = 0,05 s , keď rýchlosť lopty bola v = 5 m/s.
 
 
 
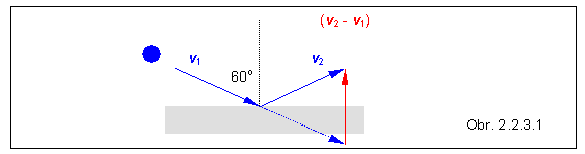
Riešenie
fstr Dt  =  m (v2 - v1)   Þ  fstr = (1/Dt ) m |(v2 -v1)|.
|(v2 - v1)| = 2v cos(60o) = 2 v . (1/2) = v = 5 m/s.
 
Pre veľkosť sily pôsobiacej na loptu tak dostaneme:
 
fstr = (1/ 0,05) . 0,2 . 5  =  20 N
 
Smer sily je zhodný so smerom rozdielu vektorov (v2 -v1).
 
 
Príklad  2.2.3.2
Proti zvislo stojacej doske strieka voda rýchlosťou  v = 20 m/s z vodorovnej hadice s prierezom q = 2,5 cm2 . Vypočítajte silu, ktorou voda pôsobí na dosku, keď hustota vody r = 1000 kg/m3.
 
Riešenie
Použijeme vzorec (2.2.3.4) , pričom si musíme uvedomiť, že ak do vzorca dosadíme rýchlosť prúdenia vody, dostaneme silu pôsobiacu na vodu zo strany dosky. Sila pôsobiaca na dosku je reakcia na ňu, takže je rovnako veľká, ale má opačný smer. Po tejto úvahe stačí použiť vzorec v skalárnej modifikácii. Keďže voda prúdi stálou rýchlosťou, pôsobiaca sila sa s časom nemení, takže namiesto derivácie môžeme napísať:
 
f  =  (Dp / Dt )  = D(m v) / Dt
 
Treba vypočítať zmenu hybnosti D(m v) prúdiacej vody pripadajúcu na časový interval  Dt . Za časový interval  Dt  dopadne na stenu objem vody (q v Dt) , po jeho vynásobení hustotou  r  získame príslušnú  hmotnosť. Pri dopade na stenu voda stráca celú horizontálnu rýchlosť, takže príslušná zmena hybnosti je
( q v Dt r)v  .  Keď zmenu vydelíme príslušným časovým intervalom, získame silu, ktorou doska pôsobí na vodu, resp. naopak:
 
f  =  ( q v Dt r) v / Dt   =  q v2 r  =  2,5 . 10-4 m2 . 400 m2/s2 . 1000 kg/m3 =  100 N
 
           
Moment hybnosti a moment sily
Pri pohybe častice po kružnici, namiesto hybnosti má praktický význam používať veličinu moment hybnosti , označovanú písmenom  L , ktorá sa zavádza vzťahom
 
L  =  r  x  mv  =   r  x  p        (2.2.3.6) 
 
Ako vidno aj na obrázku, takto zavedený vektor momentu hybnosti je kolmý na rovinu kružnice.
 
 
 
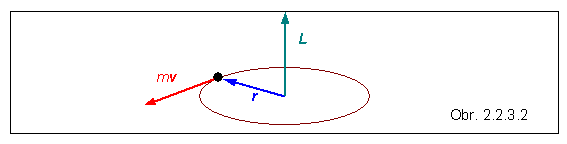
Praktický význam tejto veličiny si možno priblížiť prípadom otáčajúcej sa dvojice hmotných bodov - symetricky umiestnených na opačných koncoch priemeru kružnice (činka otáčajúca sa okolo osi prechádzajúcej jej geometrickým stredom).  Súčet vektorov hybnosti týchto dvoch bodov sa rovná nule, ale ako sa ľahko sami presvedčíte, vektorový súčet  ich momentov hybnosti sa nerovná nule. Preto je táto veličina vhodná na opis otáčajúcich sa sústav (zotrvačníkov a pod.).
Derivácia momentu hybnosti podľa času sa rovná ďalšej významnej veličine –momentu sily  M  (niekedy sa označuje aj písmenom  D):
 
 M  =   r  x  f ,        (2.2.3.7)
 
čo vidno z nasledujúceho postupu :  
 
(2.2.3.8)
 
pričom  sme využili skutočnosť, že vektory  v  a  mv  sú rovnobežné, takže ich vektorový súčin sa rovná nule. Rovnicu  (2.2.3.8) možno vysloviť : Moment sily pôsobiaci na hmotný bod sa rovná časovej zmene momentu hybnosti. (Inými slovami: Moment sily pôsobiaci na hmotný bod sa rovná zmene momentu hybnosti za jednotku času). Úpravou rovnice (2.2.3.8) do tvaru
 
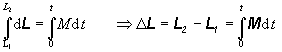        (2.2.3.9)
 
dostaneme II. vetu impulzovú pre hmotný bod. Pre izolovanú sústavu, v ktorej nepôsobia vonkajšie sily, je moment vonkajších síl nulový a následne zmena  momentu hybnosti častice je nulová. Znamená to, že pre izolovaný systém moment hybnosti   sa zachováva, takže platí  L1 = L2.
Pôsobiaca sila  f  môže mať v rovine kružnice dve zložky - rovnobežnú s polohovým vektorom a kolmú naň :
                                               
f  =  f r  +  f k
 
 
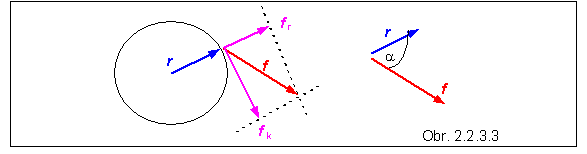
Pri pohybe častice viazanej pevne na kružnicu sa uplatní len zložka kolmá na polohový vektor častice. Pre moment takejto sily platí
                                                 
M  =  r  x  (f r  +  f k)  =  r  x  f k
 
lebo  vektorový súčin rovnobežných vektorov  r  a  f r  sa rovná nule.
 
Vo všeobecnosti platí, že veľkosť momentu sily závisí od sínusu uhla, ktorý zvierajú vektory   r  a  f:
 
M  =  r f  sin (a)                (2.2.3.10)
 
Poznámka  
Podrobnejší opis veličín moment hybnosti a moment sily je uvedený vo štvrtej kapitole v náväznosti na tuhé teleso. 
 
 

Kontrolné otázky

  1. Definujte veličinu impulz sily.
  2. Napíšte jednotku impulzu sily pomocou základných jednotiek  SI sústavy.
  3. Aký účinok sily vyjadruje veličina impulz sily?
  4. Vyjadrite impulz sily, ak pôsobiaca sila je konštantná.
  5. Vyjadrite impulz sily, ak pôsobiaca sila  nie je konštantná.
  6. Definujte hybnosť a napíšte jej rozmer.
  7. Matematicky formulujte a vysvetlite prvú vetu impulzovú.
  8. Definujte veličinu moment hybnosti  hmotného bodu , napíšte jej matematické vyjadrenie,  určite jej smer a rozmer v SI sústave.
  9. Definujte veličinu moment sily  a vysvetlite jej fyzikálny význam
  10. Aká veličina určuje  mieru otáčavého účinku sily? Napíšte jej rozmer.
  11. Môžeme vyjadriť moment sily v jednotkách J (joul)?
  12. Vysvetlite, za akých podmienok môže byť moment sily M = 0.
  13. Vyslovte a napíšte druhú vetu impulzovú pre hmotný bod.
  14. Ak sa hmotný bod nachádza v izolovanom systéme, čo možno povedať o jeho hybnosti?
  15. Ak sa hmotný bod nachádza v izolovanom systéme, čo možno povedať o jeho momente hybnosti?