Dynamika sústavy - 1. pohybová rovnicaDynamika sústavy - 1. pohybová rovnica

Sily, ktoré pôsobia na sústavu hmotných bodov (častíc) možno rozdeliť na sily vonkajšie  a vnútorné. Pod vonkajšími silami budeme rozumieť sily, ktoré majú príčinu v pôsobení okolitých telies, ktoré do sústavy hmotných bodov nepatria, ale pôsobia na  jednotlivé častice sústavy ( i = 1, ..., n) .  Výslednicu vonkajších síl pôsobiacich na i-tu časticu označme Fi.
 
Sily vnútorné majú podstatu vo vzájomnom pôsobení jednotlivých častíc sústavy. Charakterizujú interakcie medzi jednotlivými časticami vo vnútri sústavy. Označme symbolom  fij tú vnútornú silu, ktorou  pôsobí  j-ta častica na i-tu časticu a symbolom  Fvi výslednicu všetkých vnútorných síl pôsobiacich na i-tu časticu od okolitých častíc. Fvi bude určená vzťahom
 
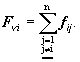        (3.1.2.1)
 
Celková sila pôsobiaca na i-tu častica Fci je súčtom celkovej vonkajšej sily a celkovej vnútornej sily pôsobiacej na i-tu časticu, t.j.
 
        (3.1.2.2)
 
Podľa druhého Newtonovho princípu platí rovnica
 
(3.1.2.3)
 
v ktorej  a i  je zrýchlenie  i - teho hmotného bodu, ktorým sa pohybuje pod vplyvom vonkajších aj vnútorných síl, pričom sumáciu treba vykonať cez všetkých  n   hmotných bodov sústavy. Takáto rovnica platí pre každý z  n  hmotných bodov sústavy. Zaujímavé výsledky získame, ak tieto rovnice sčítame :
 
(3.1.2.4)
 
V dvojitej sumácii vystupujú sily - akcia a reakcia medzi ľubovoľnou dvojicou hmotných bodov. Preto dvojitá sumácia sa rovná nule, lebo podľa zákona akcie a reakcie  f ij = -f ji . Rovnica (3.1.2.4)  sa takto zjednoduší, nevystupujú v nej vnútorné sily:
 
(3.1.2.5)
 
pričom súčet vonkajších síl pôsobiacich na sústavu sme označili písmenom  F . Rovnicu (3.1.2.5)  možno interpretovať nasledovne: Zmenu pohybového stavu sústavy hmotných bodov (častíc) spôsobuje sila F, ktorá sa rovná vektorovému súčtu vonkajších síl pôsobiacich na sústavu.
Rovnicu (3.1.2.5) možno za určitých podmienok ďalej upravovať. Treba pritom rozlíšiť, o aký druh pohybu sústavy ide. Ak všetky hmotné body sústavy majú v ľubovoľnom časovom okamihu rovnaké rýchlosti, t.j. platí  vi =  v  pre  i  =  1, ... n ,  potom aj  ai  =  a . Takýto pohyb nazývame  translačný , lebo pri ňom sa teleso v danej (inerciálnej) sústave premiestňuje bez otáčania  obr. (3.1.2.1) . Vtedy možno rovnicu (3.1.2.5)  ďalej zjednodušiť : na ľavej strane zrýchlenie vyňať pred sumačné znamienko, za ktorým zostane súčet hmotností
 
 
 
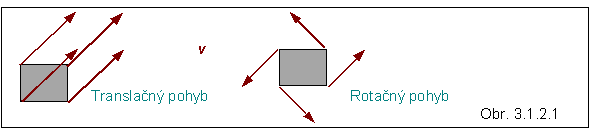
hmotných bodov sústavy, ktorý  sme v rovnici  (3.1. 1.4)  označili  M. Keď aj namiesto súčtu vonkajších síl  budeme písať  F ,  rovnica prejde do jednoduchého tvaru 
                                                
M a    =   F        (3.1.2.6)      
 
Rovnica (3.1.2.6)  je pohybová rovnica sústavy hmotných bodov pri translačnom pohybe. Ak pohyb nie je translačný, treba pri odvodení pohybovej rovnice využiť definíciu hmotného stredu  sústavy. Využijeme rovnicu  (3.1.1.3) 
 
 
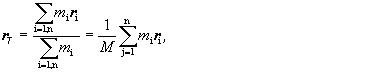
ktorú budeme dvakrát derivovať podľa času:
 
 
pričom sme využili rovnosť (3.1.2.5). Druhá derivácia polohového vektora hmotného stredu   na ľavej strane rovnice predstavuje zrýchlenie hmotného stredu   aT , takže výsledok možno napísať v
 
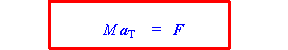(3.1.2.7)
                                                                                             
 
Odvodená rovnica predstavuje vetu o pohybe hmotného stredu (ťažiska) , ktorú môžeme slovne takto formulovať:
 
"Ťažisko sústavy hmotných bodov sa pohybuje tak, ako by v ňom bola sústredená hmotnosť celej sústavy a pôsobila naň výslednica všetkých vonkajších síl pôsobiacich na sústavu".
 
Dôsledkom tejto vety je i skutočnosť:
 
Ak sa výsledná sila pôsobiaca na sústavu rovná nule,  hmotný stred sústavy hmotných bodov zotrváva v pokoji , alebo v rovnomernom priamočiarom pohybe.
 
Pohybová rovnica (3.1.2.5), ktorá platí pre ľubovoľný pohyb sústavy hmotných bodov,  sa upravuje tak aby v nej vystupovala hybnosť sústavy hmotných bodov, čím sa rozumie vektorový súčet hybností jednotlivých bodov sústavy  (H = H1 + H2 + .... + Hn ) :
 
(3.1.2.8)
 
 
 
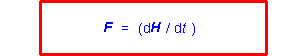
Tak sme dostali významnú rovnicu  (3.1.2.8), ktorá sa nazýva prvá pohybová rovnica pre sústavu hmotných bodov.  Jej slovná formulácia hovorí, že:
 
súčet všetkých vonkajších síl pôsobiacich na sústavu hmotných bodov sa rovná derivácii hybnosti sústavy .
 
Integráciou tejto pohybovej rovnice získame  prvú impulzovú vetu:
 
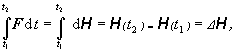        (3.1.2.9)
                                                                                                           
ktorá hovorí, že impulz vonkajšej sily pôsobiaci na sústavu hmotných bodov sa rovná zmene hybnosti sústavy. Táto veta je formálne, ale aj obsahom v priamom vzťahu so vzorcom (2.2.3.5)  paragrafu o impulze a hybnosti hmotného bodu.
 
Ak výslednica všetkých vonkajších  síl pôsobiacich na sústavu je nulová (F = 0), hovoríme, že sústava je izolovaná. V tomto prípade rovnica (3.1.2.9) prejde na tvar      
 
D H = 0   Þ   H1 = H2        (3.1.2.10 )

ktorá vyjadruje zákon zachovania celkovej hybnosti izolovanej sústavy hmotných bodov a možno ju vysloviť:

Zmena celkovej hybnosti izolovanej sústavy hmotných bodov je nulová, hybnosť izolovanej sústavy sa nemení.
           
 
Poznámka  
Ak výsledná sila pôsobiaca na sústavu (t.j. súčet všetkých vonkajších síl) sa rovná nule, to ešte neznamená, že sa nemôžu meniť hybnosti jednotlivých hmotných bodov sústavy. Môžu sa meniť pod účinkom vnútorných, ale aj vonkajších síl tak, aby vektorový súčet ich zmien bol nulový. Ako príklad môže poslúžiť výbuch pokojne ležiaceho granátu. Ak je granát v našej inerciálnej sústave v pokoji, výslednica vonkajších síl sa rovná nule. Pri výbuchu sa uplatnia vnútorné sily, časti granátu sa rozletia, ale ťažisko celej sústavy naďalej zostáva v pokoji.
 
 
Príklad  3.1.2.1
Na pokojnej hladine jazera sa nachádza v pokoji loďka s hmotnosťou M , na jej jednom konci stojí  plavčík s hmotnosťou  m . Plavčík sa začne pohybovať vzhľadom na loďku rýchlosťou  u . Vypočítajte rýchlosť plavčíka  v  a rýchlosť loďky  w  vzhľadom na breh. Predpokladajte, že loďka sa po hladine pohybuje bez trenia.
 
 
 
Riešenie 
Loďku s plavčíkom považujeme za sústavu pozostávajúcu z dvoch častí. Loďka s plavčíkom sú na začiatku vzhľadom na breh v pokoji, teda výsledná vonkajšia sila pôsobiaca na sústavu sa rovná nule.  Keď plavčík začne kráčať, začnú v sústave pôsobiť vnútorné sily medzi plavčíkom a loďkou, nie však vonkajšie sily. Preto sa hybnosť sústavy ako celku nemôže zmeniť, vzhľadom na breh musí zostať nulová. Plavčík aj loďka však vzhľadom na breh nadobudnú hybnosti   m v , resp  M w,  ktorých vektorový súčet sa musí rovnať nule, takže m v + M w = 0.  Ak má platiť takýto vzťah, vektory v  a  w  musia mať opačný smer, preto v  = v  j  a  w = - w j . Po dosadení do rovnice a jej skalárnom súčine s vektorom  j  dostaneme  m v  - M w = 0  Þ   v /w = M /m .  Medzi rýchlosťami  u, v , w  platí vzťah v = u + w , ktorý vyplýva zo vzorca pre rýchlosť pri zloženom pohybe (vzorec 2.1.10.5), keď jednu vzťažnú sústavu viažeme na breh a druhú na loďku .  Po skalárnom súčine tejto rovnice s jednotkovým vektorom  j  dostaneme skalárnu rovnicu   v   =  u  -  w  pre veľkosti rýchlostí.  Túto rovnicu spojíme so skalárnou rovnicou pre hybnosti, čím dostaneme  rovnicu  Mw = m(u - w), z ktorej vypočítame  w = mu / (m + M)  a  po dosadení do vzťahu medzi rýchlosťami aj  v  =  Mu / (M + m).
 
 
Príklad  3.1.2.2
Na pokojnej hladine jazera sa nachádza v pokoji loďka s hmotnosťou M  a dĺžkou  L, na jej jednom konci stojí  plavčík s hmotnosťou  m . Vypočítajte o koľko sa posunie ťažisko loďky vzhľadom na breh, ak plavčík prejde na druhý koniec loďky.
 
 
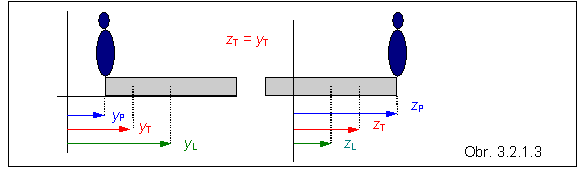
Riešenie 
Loďka a plavčík sú na začiatku v pokoji, preto v pokoji je aj ich ťažisko vzhľadom na vzťažnú sústavu viazanú na breh. Nulové je aj zrýchlenie ťažiska, čo podľa vety o ťažisku  znamená, že výsledná je aj vonkajšia sila, ktorá na sústavu loď - plavčík pôsobí. Keď sa plavčík začne pohybovať, začnú v sústave pôsobiť vnútorné sily, vonkajšia zostáva nulová. Preto zrýchlenie ťažiska sústavy bude naďalej nulové, ťažisko nezmení svoju polohu. Na obrázku 3.2.1.3 sú vyznačené začiatočné súradnice plavčíka yP , stredu (ťažiska) loďky  yL  a ťažiska sústavy  yT  a súradnice po presunutí plavčíka, označené pre ľahšie rozlíšenie písmenami  z . Na začiatku pre súradnicu ťažiska sústavy platí
 
yT  = (myP + MyL) / (m + M )
 
Výpočet si zjednodušíme, ak začiatok na súradnicovej osi zvolíme tak, aby  yP = 0 .  Potom sa zjednoduší aj vyjadrenie polohy stredu loďky : yL =  L / 2 , takže
 
yT  = M (L /2) / (m + M )
 
Po presunutí plavčíka  zP = zL + L /2 , takže
 
 zT = (mzP + MzL) / (m + M ) = [m(zL + L /2) + MzL ] /(m + M )
 
Teraz využijeme podmienku  zT  =  yT  , dosadíme na ľavú stranu rovnice, čím vznikne rovnica
           
[m(zL + L /2) + MzL ] = M (L /2)
 
v ktorej jedinou neznámou hodnotou je  zL ,  pre ktorú dostaneme výsledok
         
zL  =  [(M - m)(L /2)] / ( m + M )
 
Rozdiel  yL  - zL  predstavuje hľadané posunutie ťažiska loďky.
 
 
Príklad 3.1.2.3
Na skyborde o hmotnosti m,  ktorý sa pohybuje konštantnou rýchlosťou  v0 stojí dievča o hmotnosti m1  a  v  ruke drží sklenenú guľu s hmotnosťou m2.. . Sklenená guľa sa náhle roztrhne na dve časti, pričom časť gule  s hmotnosťou m21 odletela rýchlosťou v21 opačným smerom ako pohybujúci sa skybord, Druhá časť gule s hmotnosťou m22 sa pohybovala rýchlosťou v22 v smere zvierajúcim  s pohybujúcim sa skybordom uhol a. Dievča v okamžiku roztrhnutia gule od ľaku zoskočí zo skybordu v opačnom smere pôvodného  pohybu skybordu rýchlosťou v2.  Určite rýchlosť v1 prázdneho skybordu, , ktorou sa pohyboval v okamžiku roztrhnutia gule.
 
 
 
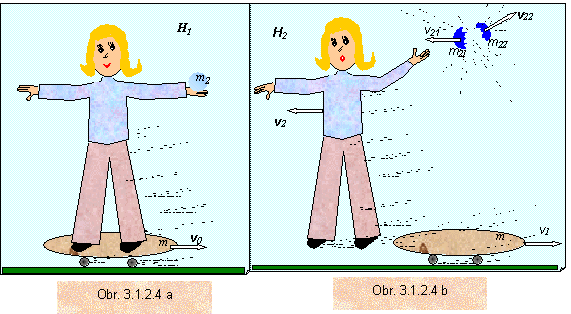
Riešenie
Sústava častíc, ktorú skúmame sa skladá na začiatku skúmania  zo skybordu, na ktorom sa vezie  dievča s guľou. Označme hybnosť tejto sústavy H1.  Po roztrhnutí gule sústava sa skladá z pohybujúceho sa dievčaťa s hybnosťou  H,   pohybujúceho sa vozíka s hybnosťou H2   a pohybujúcich sa dvoch častí gule s hybnosťami H21 a H22.   Ak zanedbáme silu trenie skybordu a odporu vzduchu, na každú časť sústavy pôsobí len  tiažová sila. Keďže tiažová sila má zvislý smer, neprispieva k zmene vodorovnej zložky celkovej hybnosti sústavy. Vodorovná (x -ová) zložka hybnosti sústavy sa zachováva  a platí pre ňu zákon zachovania hybnosti, t.j. vodorovná zložka hybnosti sústavy pred roztrhnutím gule sa rovná vodorovnej zložke hybnosti sústave v okamžiku roztrhnutia gule. Matematické vyjadrenie zákona zachovania hybnosti v súradnicovej sústave s kladnou osou x v smere pohybu skybordu pred roztrhnutím gule je dané rovnicou
 
H1x= Hx + H2x+ H21x + H2x        (1)
 
Po dosadení x-vých zložiek jednotlivých rýchlostí pred roztrhnutím : v0 = [ v0, 0 ] a po roztrhnutí:
 
v 1 = [ v1, 0 ] , v 21 = [- v 21, 0 ], v 22 = [ v 22  cos a ,  v 22  sin a ], v 2 = [- v 2,, 0 ] 
 
do rovnice (1) dostaneme
 
 
 
odkiaľ vyjadríme rýchlosť prázdneho skybordu v1
 
 

Kontrolné otázky

  1. Definujte hybnosť sústavy hmotných bodov a vyjadrite ju v matematickom tvare.
  2. Definujte  a zapíšte výslednicu všetkých síl pôsobiacich na sústavu hmotných bodov. Význam jednotlivých členov vysvetlite.
  3. Napíšte pohybovú rovnicu pre sústavu hmotných bodov, ktorej všetky body konajú translačný pohyb.
  4. Vyslovte a zapíšte vetu o pohybe ťažiska.
  5. Kedy hmotný stred sústavy hmotných bodov koná rovnomerný priamočiary pohyb?
  6. Vyslovte a matematicky formulujte prvú pohybovú rovnicu pre sústavu hmotných bodov.
  7. Vyslovte a zapíšte I. vetu impulzovú pre sústavu hmotných bodov.
  8. Vyslovte zákon zachovania hybnosti pre  izolovanú sústavu hmotných bodov.
  9. Uveďte príklad, kde sa aplikuje zákon zachovania hybnosti.
  10. Akým spôsobom je možné pohnúť sa na  dokonale hladkom ľade?
  11. Z platnosti akého zákona sme vychádzali  v príklade 3.1.2.3 .
  12. Prečo sme v príklade 3.1.2.3  formulovali zákon zachovania hybnosti len pre  x - ovú zložku celkovej hybnosti sústavy?
  13. Možno aplikovať zákon zachovania hybnosti v príklade 3.1.2.3 aj na y - ovú zložku celkovej hybnosti sústavy? Svoju odpoveď zdôvodnite.