 Práca v gravitačnom poli, potenciálna energia
Práca v gravitačnom poli, potenciálna energia
Predpokladajme, že hmotný bod o hmotnosti M je zdrojom gravitačného poľa. V určitom mieste poľa s polohovým vektorom r vzhľadom na bod M nech sa nachádza iný hmotný bod s hmotnosťou m. Vieme už, že príťažlivá sila, ktorá na tento hmotný bod pôsobí je
Ak chceme hmotný bod m premiestniť z bodu 1 s polohovým vektorom r1 do bodu 2 s polohovým vektorom r2 (obr. 3.2.4.1), musíme túto silu prekonávať silou
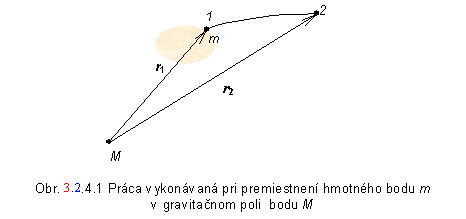
a vykonáme pritom prácu
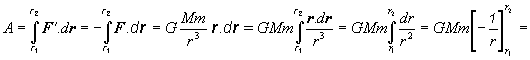
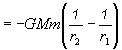 (3.2.4.3)
(3.2.4.3)(r1, r2 a dr sú veľkosti príslušných vektorov r1, r2 a dr).
Z výsledku vidíme, že práca nezávisí od toho, po akej dráhe sa hmotný bod m premiestnil z bodu 1 do bodu 2. Práca je úplne určená počiatočnou a konečnou vzdialenosťou prenášaného hmotného bodu m od nehybného bodu M, ktorý je zdrojom poľa.
V uvažovanom prípade sme hmotný bod m od zdroja gravitačného poľa vzďaľovali, takže prácu konala určitá vonkajšia sila premáhaním síl gravitačného poľa. Ak sa pohyb deje v opačnom smere, prácu koná gravitačné pole.
Hmotný bod má teda v dôsledku existencie gravitačnej sily schopnosť konať prácu. Hovoríme, že má polohovú alebo potenciálnu energiu.
Potenciálna energia hmotného bodu s hmotnosťou m v polohe určenej polohovým vektorom r0 v poli hmotného bodu M je teda rovná
Najvhodnejšie je voliť vzťažnú polohu vo vzdialenosti nekonečne veľkej, t.j. r0 = ¥. Potenciálna energia vzhľadom na nekonečno je potom daná vzťahom
Číselne sa táto potenciálna energia v zmysle vzťahu (3.2.4.4) rovná práci, ktorú musíme vykonať, aby sme hmotný bod m v poli hmotného bodu M premiestnili z daného bodu do nekonečna.
Kontrolné otázky
-
Čomu sa rovná práca, vykonaná pri premiestnení hmotného bodu m v gravitačnom poli hmotného bodu M z miesta s polohovým vektorom r1 do miesta r2 (polohové vektory sú vzťahované vzhľadom na gravitačné centrum)?
-
Čo je to potenciálna energia? Voči akému miestu ju najčastejšie vzťahujeme?
