Dokonale tuhé teleso je teleso, ktoré sa pôsobením síl nedeformuje, t. j. vzdialenosti medzi jeho jednotlivými časťami sa zachovávajú. Pretože v tejto kapitole sa budeme zaoberať len dokonale tuhým telesom, budeme používať skrátený názov tuhé teleso. Môžeme si ho predstaviť ako sústavu veľkého počtu bodov, ktoré sa z hľadiska makroskopického javia ako teleso so spojito rozloženou hmotnosťou s hustotou (objemovou hmotnosťou) r, definovanou všeobecne pre nehomogénne teleso ako funkcia miesta daná podielom hmotnosti veľmi malej časti objemu a tohoto objemu:

 

        (4.1.1.1)

 

Počet stupňov voľnosti 3N pre N hmotných bodov sa pre teleso znižuje počtom väzieb. Tuhé teleso má len maximálne 6 stupňov voľnosti, jeho poloha je určená polohou troch bodov neležiacich na jednej priamke, pričom ich vzdialenosti sú pevne dané.

 

Dôležitým bodom tuhého telesa je jeho hmotný stred. Jeho definícia vychádza z definície hmotného stredu sústavy hmotných bodov, len ich hmotnosti sú nahradené hmotným elementom dm a sumácie integrálom. Polohový vektor hmotného stredu je preto daný vzťahmi:

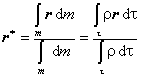        (4.1.1.2)

 

Hmotný stred je totožný s ťažiskom telesa, ktoré je definované ako pôsobisko tiažovej sily v homogénnom tiažovom poli pri ľubovolnom otočení telesa.

 

Pre popis pohybu voľného tuhého telesa potrebujeme dve vektorové rovnice: prvú a druhú pohybovú rovnicu. Sú to diferenciálne rovnice druhého rádu, pre jednoznačné riešenie stavu telesa potrebujeme zadať počiatočné podmienky, štyri vektorové údaje.