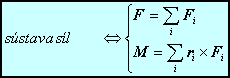Sily, pôsobiace v tuhom telese sú sily objemové (napr. tiaž), sily plošné (napr. tlakové sily) a sily pôsobiace v bode t. j. sily, pre ktoré oblasť pôsobenia je malá v porovnaní s rozmermi telesa. Moment sily vieme vyjadriť len pomocou bodového pôsobiska sily. Objemové sily môžeme vyjadriť pomocou nekonečného súčtu elementárnych síl dF pôsobiacich na element objemu dt (u plošných síl na element plochy dS) - teda bodových síl. Aby sme mohli riešiť pohybové rovnice, nahradzujeme tieto sily jednou, pôsobiacou v bode. Napr. tiaž, pôsobiaca v ťažisku je súčtom jednotlivých elementárnych tiažových síl pôsobiacich na elementy hmotnosti dm. Z praktického hľadiska, napr. aby sme určili reakcie dotýkajúcich sa telies v statike, aby sme zostavili jednoducho pohybové rovnice, potrebujeme sily v telese premiestňovať, tak aby sme ich mohli vektorovo sčítať. Všeobecne hovoríme o redukcii síl. Redukcia síl je teda nahradenie sústavy síl jednou silou a jedným momentom sily tak, aby sa tým nezmenil účinok týchto síl.

 

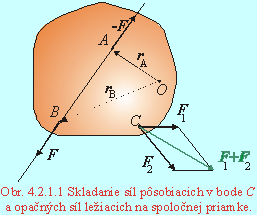
Sily pôsobiace v jednom bode skladáme na základe princípu superpozície - výsledná sila je vektorovým súčtom síl, pôsobisko sa nemení (Obr.4.2.1.1 skladanie síl  v bode C). Zložitejší prípad nastáva, ak sily pôsobia v rôznych bodoch a naviac ležia na priamkach, ktoré sú napr. mimobežné. Vyjdime z vlastnosti dokonale tuhého telesa, že je nedeformovatelné. Ak v dvoch rôznych bodoch A a B budú pôsobiť rovnako veľké opačne orientované sily ležiace na jednej priamke (táto priamka prechádza pôsobiskami síl), ich účinky sa rušia. Aj momenty týchto síl sú rovnako veľké, opačne orientované (Obr.4.2.1.1. sily v bode A a B).

 

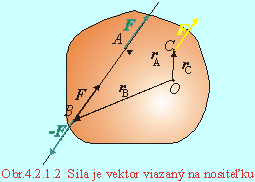
Na základe tejto vlastnosti tuhého telesa môžeme posúvať silu po priamke na ktorej sila leží (vektorová priamka) - v tuhom telese je sila vektorová veličina viazaná na priamku. Vysvetlenie plynie z Obr.4.2.1.2. Na teleso pôsobí sila F v bode A . Pridaním síl F a  - F pôsobiacich v bode B sa nemení pôsobenie síl. Ale podľa predchádzajúceho, sa navzájom rušia aj sila F pôsobiaca v bode A so silou - F pôsobiacou v bode B. Výsledná sila je preto sila F posunutá do bodu B.  Silu ale nemôžeme presunúť do bodu C , ktorý leží mimo vektorovej priamky: jednak  pre body A a C neplatí rušenie sily F silou  - F, jednak len  presunutím sily z bodu A do bodu B sa moment sily nemení (presunutím do bodu C sa jej moment zmení).

 

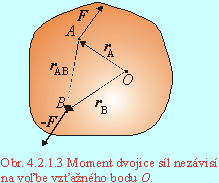
Špeciálnou sústavou síl je dvojica síl. Dvojica síl sú dve sily rovnako veľké, opačného smeru, neležiace na jednej priamke. Pre dvojicu síl platí, že jej výsledný moment sily nezávisí od voľby vzťažného bodu. Moment dvojice síl  je voľný vektor, môžeme ho presunúť do ľubovolného bodu.

 

Dôkaz vyplýva z Obr.4.2.1.3. Pre celkový moment platí:

 

 

Posledný výraz nezávisí od voľby bodu O.

 

 

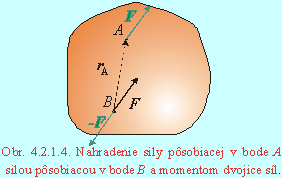
Na základe predchádzajúcich úvah možno sústavu síl pôsobiacich na tuhé teleso redukovať, nahradiť jednoduchším vyjadrením veličín spôsobujúcich zmenu pohybového stavu. Aby sme mohli pohyb tuhého telesa pod účinkom síl riešiť jednoducho, často je vhodné vyjadriť silové pôsobenie v konkrétnom bode (napr. v mieste závesu, v ťažisku). Spôsob redukcie síl je zrejmý z Obr. 4.2.1.4. Nech sila F pôsobí v bode A. Úlohou je premiestniť všetky sily a teda aj silu F do bodu B a tým redukovať ich počet. Pridajme do bodu B sily F a - F, tým sa nič nezmenilo. Sila F pôsobiaca v bode A a sila - F pôsobiaca v bode B tvoria dvojicu síl s momentom dvojice síl daný voľným vektorom.

 

 

Namiesto sily pôsobiacej v bode A máme rovnakú silu pôsobiacu v bode B a voľný vektor momentu pôvodnej sily vzhľadom na bod B. Takto môžeme premiestniť do bodu B každú zo síl pôsobiacich v rôznych bodoch telesa.