Z technického hľadiska je dôležitý pohyb tuhého telesa okolo pevnej osi. Než vyjadríme rovnice opisujúce tento pohyb, hľadajme zásadné vlastnosti týchto rovníc. Predovšetkým všetky body telesa, a teda aj hmotný stred, vykonávajú pohyb po kružnici so stredom na osi otáčania (často sa hmotný stred nachádza na osi, takže sa nepohybuje). Pohyb telesa okolo pevnej osi je pohyb s jedným stupňom voľnosti. Týmto časovo závislým parametrom môže byť uhol pootočenia telesa okolo osi. Rotáciu charakterizujú kinematické veličiny rotačného pohybu, uhol otočenia j , uhlová rýchlosť w a uhlové zrýchlenie e. Riešenie nájdeme riešením jednej zložky pohybových rovníc. Pretože výsledná sila je nulová v prípade , že hmotný stred leží na osi, (plynie z vety o pohybe hmotného stredu, zo vzťahu (4.2.2.7)), riešenie musí vychádzať z jednej zložky druhej pohybovej rovnice. Zvoľme si vzťažný bod na osi otáčania. Ďalej predpokladajme, že os je pevná, t. j. sily pôsobiace na teleso sú kompenzované silami upevnenia osi tak, že nedochádza k zmene osi otáčania. Rozložme moment sily pôsobiaci na teleso

 

 

na dve zložky: do smeru rovnobežného s osou a do smeru kolmého na os. Jednoduchým pokusom sa môžete presvedčiť, že moment sily kolmý na os (tvorený silou rovnobežnou s osou), namáha os, musí byť kompenzovaný pevnosťou osi a jej uloženia. Moment sily rovnobežný s osou  naopak mení pohybový stav telesa. Nemôže byť kompenzovaný momentmi síl pôsobiacimi na os, pretože tie sú kolmé na os - ich polohový vektor vzhľadom na vzťažný bod leží v osi otáčania a moment sily je kolmý na tento vektor. Pohybovou rovnicou, ktorá opisuje rotáciu telesa okolo osi je preto priemet druhej pohybovej rovnice do osi otáčania. Všeobecne priemet vektora x do smeru jednotkového vektora r je vektor, daný vzťahom:

 

 

 - jeho súradnica je daná skalárnym súčinom a vektor má smer vektora r. Pohybovú rovnicu (4.2.2.8) môžeme prepísať (vektor r je jednotkový vektor v smere osi otáčania):

 

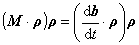        (4.2.4.1)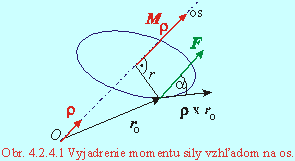

 

Definujme moment sily vzhľadom na os

 

,         

 

moment sily vzhľadom na os je vektorová veličina daná priemetom momentu sily vzhľadom na bod, ktorý je na osi otáčania, do osi otáčania.

Jeho veľkosť je daná súčinom kolmej vzdialenosti sily od osi otáčania a zložky sily kolmej na rovinu preloženú osou a bodom pôsobiska sily (Obr. 4.2.4.1):

 

 

Z tejto skutočnosti vyplýva, že moment sily vzhľadom na os nezávisí od voľby vzťažného bodu na osi, je to vektorová veličina viazaná na os.

Vyjadrime teraz pravú stranu rovnice (4.2.4.1).

Zaveďme pojem moment zotrvačnosti

 

        (4.2.4.2)

 

integrál zo štvorcov kolmej vzdialenosti hmotného elementu od danej osi cez celú hmotnosť telesa (r sme zaviedli ako kolmá vzdialenosť elementu hmotnosti od osi otáčania). Potom

dosadením do rovnice (4.2.4.1) dostávame pohybovú rovnicu pre otáčanie telesa okolo osi

 

        (4.2.4.3)

 

na teleso pôsobiaci moment sily vzhľadom na os sa rovná súčinu momentu zotrvačnosti telesa vzhľadom na túto os a uhlového zrýchlenia.  

Odvodenie tohoto vzťahu je v časti: Odvodenie pohybovej rovnice pre rotačný pohyb okolo pevnej osi

Ak porovnáme túto rovnicu s rovnicou pohybu hmotného bodu

 

 

vidíme analógiu pohybov, s tým, že moment zotrvačnosti je mierou zotrvačných vlastností rotujúceho telesa. Moment zotrvačnosti je dôležitou veličinou pre rotáciu telies.

Pri jeho výpočte môžeme využiť niektoré jeho vlastnosti.

Moment zotrvačnosti hmotného bodu hmotnosti m vo vzdialenosti r od osi je

 

 

Moment zotrvačnosti sústavy hmotných bodov (i-ty hmotný bod vo vzdialenosti r_i od osi má hmotnosť m_i ) je

 

 

Steinerova veta. Telesom, ktorého moment zotrvačnosti určujeme, veďme dve rovnobežné osi, ktorých vzdialenosť je a. Jedna prechádza hmotným stredom telesa a moment zotrvačnosti vzhľadom na ňu je  J^* . Potom moment zotrvačnosti J vzhľadom na druhú os  je:

 

        (4.2.4.5)

 

kde m je hmotnosť telesa.

 

Moment zotrvačnosti vzhľadom na ľubovoľnú os sa rovná momentu zotrvačnosti vzhľadom na os, ktorá je s ňou rovnobežná a prechádza hmotným stredom, zväčšenému o moment zotrvačnosti hmotného bodu o hmotnosti rovnajúcej sa hmotnosti telesa a nachádzajúceho sa vo vzdialenosti rovnej vzájomnej vzdialenosti osí.

 

Dôkaz Steinerovej vety vyplýva z jednoduchej transformácie súradníc a vlastnosti hmotného stredu. Pre jednoduché homogénne telesá môžeme z definície a Steinerovej vety vypočítať momenty zotrvačnosti.

 

Valec hmotnosti m  s polomerom r vzhľadom na geometrickú os

 

Valec hmotnosti m s polomerom r vzhľadom  na obvodovú priamku
Dutý valec hmotnosti m s vonkajšim polomerom r1 a vnútorným polomerom r2 vzhľadom na geometrickú os
Tyč hmotnosti m a dĺžky l zanedbateľného prierezu vzhľadom na os kolmú na tyč: prechádzajúcu koncovým bodom tyče
Tyč hmotnosti m a dĺžky l zanedbateľného prierezu vzhľadom na os kolmú na tyč: prechádzajúcu stredom tyče
Guľa hmotnosti m a polomeru r vzhľadom na os prechádzajúcu jej stredom