Energia je aditívnou veličinou jej častí, t. j.  pre sústavu častíc je celková energia súčtom energií jej častíc. Na základe tohoto princípu vyjadrime kinetickú energiu tuhého telesa.

Kinetická energia hmotného elementu dm je daná jeho rýchlosťou v:

 

 

a celková kinetická energia telesa je integrálom cez celú hmotnosť telesa:

 

        (4.2.5.1)

 

 

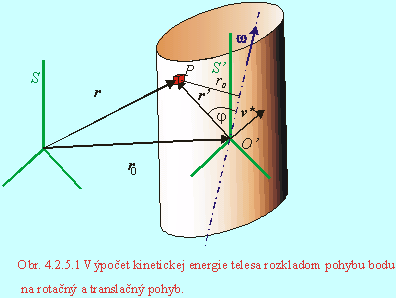
Výpočet kinetickej energie telesa uľahčí rozloženie pohybu telesa na translačný a rotačný pohyb (Obr.4.2.5.1). Zvoľme si hmotný stred ako vzťažný bod  pohybujúci sa rýchlosťou v^* (určuje translačný pohyb telesa). Potom po dosadení za rýchlosť hmotného elementu dm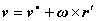 

do vzťahu pre kinetickú energiu platí:

 

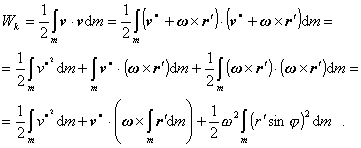                (4.2.5.2)

 

Prvý člen vyjadruje kinetickú energiu translačného pohybu:

 

 

druhý člen je nulový, pretože hmotný stred v sústave S´ je v začiatku, t. j.

 

 

posledný člen vyjadruje kinetickú energiu rotačného pohybu vzhľadom na okamžitú os rotácie prechádzajúcu hmotným stredom:

 

        (4.2.5.3)

 

kde J^* je moment zotrvačnosti telesa vzhľadom na os prechádzajúcu hmotným stredom. Pre kinetickú energiu telesa všeobecne platí:

 

        (4.2.5.4)

 

Pre teleso, ktoré vykonáva len rotačný pohyb,  zvoľme pomocný bod na osi otáčania. Rýchlosť tohoto bodu je nulová a vo vzťahu  (4.2.5.2) je nenulový len tretí člen aj v prípade, že vzťažný bod nie je hmotný stred:

 

        (4.2.5.5)

 

Vyjadrime potenciálnu energiu telesa v homogénnom poli, t. j. v poli v ktorom intenzita poľa je konštantná veličina E = konst. Ak nulový potenciál volíme v počiatku súradnicovej sústavy, potom potenciálna energia dW hmotného elementu dm sa dá vyjadriť

 

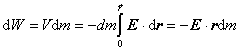
Potom potenciálna energia telesa je

 

 

Ak využijeme definíciu hmotného stredu, potom sa posledný výraz dá prepísať

 

 

Pre homogénne silové pole potenciálna energia sa rovná súčinu potenciálu v mieste hmotného stredu a hmotnosti telesa.Teleso môžeme otáčať okolo hmotného stredu a jehoh potenciálna energia sa nezmení. Napr. potenciálna energia v tiažovom poli Zeme (E = - gk)

 

kde z* je výška hmotného stredu nad vzťažnou vodorovnou rovinou.

V izolovanej sústave platí zákon zachovania mechanickej energie, napr. v tiažovom poli Zeme:

 

        (4.2.5.6)

 

V súvislosti s energiou dokonale tuhého telesa je dobré porovnať tento výsledok aj s energiou sústavy hmotných bodov, ako telesom s pružnými väzbami medzi hmotnými bodmi

 

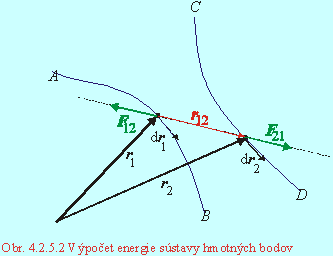
Uvedomme si, že sústava hmotných bodov nie je dokonale tuhá sústava, ako je dokonale tuhé teleso. Mechanická energia sústavy hmotných bodov, ktoré navzájom na seba silovo pôsobia, závisí aj od vzájomných vzdialeností jednotlivých hmotných bodov. Uvažujme systém dvoch častíc s hmotnosťami m₁ a m₂, na ktoré pôsobia vonkajšie sily F₁ , F₂  a vzájomné vnútorné sily F₁₁ = - F₂₁  . Tieto hmotné body sa pohybujú po dráhach  určených polohovými vektormi r₁ , r₂   (Obr. 4.2.5.2). Ich pohybové rovnice sú:

 

 

Vynásobme ich posunutím, ktoré sa uskutoční za elementárny časový interval dt a sčítajme, dostávame:

           

 

Túto rovnicu upravme: pravú stranu rovnako, ako sme upravili tento výraz pre kinetickú energiu hmotného bodu, na ľavej strane využime zákon akcie a reakcie, 

 

 

 a skutočnosť, že rozdiel posunutí je zmena vzájomnej polohy častíc:

 

 

 

Dostávame:

 

 

Integrujme túto rovnicu  od počiatočného času t₀  po čas  t. Za tento časový interval sa hmotný bod m₁ presunie po krivke C₁  (z bodu A do bodu B), jeho počiatočná rýchlosť v₁₀ sa zmení na konečnú rýchlosť v₁  a hmotný bod m₂ sa presunie po krivke C₂  (z bodu C do bodu D), jeho počiatočná rýchlosť v₂₀ sa zmení na konečnú rýchlosť v₂

 

 

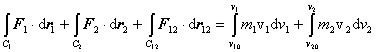
Krivka C₁₂ je daná dráhou hmotného bodu m₂, vzhľadom na hmotný bod m₁. Prvé dva členy na ľavej strane vyjadrujú prácu externých síl A_ex , tretí prácu interných síl  A_in , pravá strana zmenu celkovej kinetickej energie sústavy DW_k (Kinetická energia sústavy hmotných bodov je súčet kinetických energií všetkých hmotných bodov tvoriacich sústavu):

 

        (4.2.5.7)

 

Tuto rovnicu možno zovšeobecniť pre sústavu N  častíc. Práca  externých síl je súčtom prác všetkých externých síl, kinetická energia  sústavy je súčtom kinetických energií všetkých častíc. Práca interných síl je súčtom prác interných síl pri vzájomnom posunutí každej dvojice častíc:

 

Pre konzervatívne vnútorné sily (základné sily pôsobiace medzi elementárnymi časticami, ako sily elektromagnetické alebo gravitačné, sú sily konzervatívne) existuje fyzikálna veličina  W_p,in , ktorá je funkciou len vzájomnej polohy častíc. Nazýva sa vnútorná potenciálna energia sústavy častíc (energia systému) a vyjadruje schopnosť konať prácu pri zmene vzájomnej polohy častíc:

 

 

Nulovú potenciálnu vnútornú energiu volíme pre určitý stav sústavy, napr. pre častice navzájom tak vzdialené, že na seba silovo nepôsobia.

 

Vnútorná energia sústavy častíc (systému, v termodynamike označovaná U ) je súčet kinetickej energie častíc v súradnicovej sústave nehybného hmotného stredu a vnútornej potenciálnej energie sústavy častíc a je vyjadrená vzťahom:

 

 

kde

 

 

Rovnica (4.2.5.7) dosadením vnútornej energie nadobudne tvar

 

        (4.2.5.8)

 

a pre izolovanú sústavu častíc vyjadruje zákon zachovania vnútornej energie: V izolovanej sústave častíc sa vnútorná energia sústavy zachováva.

 

Tuhé teleso môžeme porovnať so sústavou hmotných bodov: je to sústava, ktorej vzájomný pohyb častí je obmedzený. V dokonale tuhom telese sa vzdialenosti jednotlivých bodov nemenia. V súradnicovej sústave s počiatkom v jednom z bodov telesa sa ostatné body pohybujú len rotačným pohybom. Pootočenie dj každého bodu je rovnaké. Sledujme prácu vzájomných síl dvoch elementov hmotnosti. Tieto sily sú vo vzťahu akcie a reakcie. Zo zákona akcie a reakcie ich momenty vzhľadom na ľubovoľný bod sú opačné vektorové veličiny. Pri rovnako pootočení všetkých elementov hmotnosti celkové práca týchto dvoch a teda ja všetkých vnútorných síl je nulová. Vnútorné sily nekonajú prácu, netreba zavádzať vnútornú potenciálnu energiu. Ak ide o teleso poddajné, kde je možný i relatívny pohyb, posunutie a pootočenie elementov je rôzne. Pre stlačenú pružinu má zmysel zaviesť vnútornú potenciálnu energiu, ktorá sa rovná práci vykonanej pružinou pri jej uvoľnení.