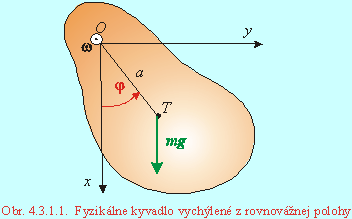
Fyzikálne kyvadlo je každé teleso, ktoré sa môže otáčať bez trenia okolo vodorovnej osi neprechádzajúcej ťažiskom. Jeho pohyb sa riadi pohybovou rovnicou (4.2.4.3), ktorá vyjadruje otáčanie tohoto telesa okolo osi. Obr. 4.3.1.1 zobrazuje stav telesa v danom okamihu, súradnicová sústava je volená tak, že x-ová os smeruje zvisle dole, y-ová  leží v rovine kývania, z-ová má smer osi otáčania, vyznačený uhol je kladný. Moment sily vzhľadom na os je vektorová veličina

 

 

        (4.3.1.1)

 

kde jednotkový vektor r v smere osi otáčania sme volili orientovaný v kladnom smere osi z, vektor momentu tiažovej sily M má opačný smer ako vektor r (skalárny súčin vo vzťahu (4.3.1.1) je záporný), a je vzdialenosť ťažiska od osi otáčania,  mg veľkosť tiažovej sily. Pretože uhlové zrýchlenie je

 

 

pohybová rovnica (4.3.1.1) má tvar

 

 

Rovnosť vektorov znamená aj rovnosť ich súradníc, t. j.

 

 

Znamienko mínus v rovnici nie je dôsledkom voľby súradnicovej sústavy, vyjadruje skutočnosť, že moment sily stáča teleso do rovnovážnej polohy s nulovým uhlom výchylky. Z hľadiska matematiky, ide o diferenciálnu rovnicu druhého rádu (najvyšší rád derivácie je druhý), s trigoniometrickou funkciou, kde analytické riešenie pre premennú j, možno vyjadriť len po rozvoji sínusovej funkcie do radu. Pre veľmi malé výchylky nahradíme sínusovú funkciu uhlom:

 

 

(„veľmi malé“ sa vzťahuje na presnosti merania výchylky a času, t. j. nepresnosti výpočtu sú podstatne menšie ako nepresnosti merania). Pohybová rovnica v tomto priblížení má tvar diferenciálnej rovnice druhého rádu s konštantnými koeficientmi bez pravej strany

 

        (4.3.1.2)

 

Riešením tejto rovnice je harmonická funkcia

 

        (4.3.1.3)

 

kde integračná konštanta F má význam amplitúdy - maximálnej výchylky uhla , a a je fázové posunutie, ktoré určuje počiatočnú výchylku (v čase t = 0):

 

 

 

Riešenie možno vyjadriť aj pomocou kosínusovej funkcie, potom fázové posunutie malo inú veľkosť.

Periódou periodickej funkcie je minimálny časový interval T po ktorom sa pohybový stav opakuje t. j.  platí

 

 

z čoho pre funkciu (4.3.1.3) plynie:

 

 

Perióda (doba kmitu) fyzikálneho kyvadla je:

 

        (4.3.1.4)

 

Matematické kyvadlo je model fyzikálneho kyvadla, kde kmitajúce teleso je nahradené hmotným bodom s hmotnosťou m, viazaným v pevnej vzdialenosti a od bodu upevnenia. Prakticky je to teleso s malými rozmermi (vzhľadom na vzdialenosť od osi) zavesené na pevnom vlákne zanedbateľnej hmotnosti. Je to teda fyzikálne kyvadlo s momentom zotrvačnosti ma². Jeho doba kmitu po dosadení do vzťahu (2.4.25) je

 

 

Torzné kyvadlo je teleso zavesené na pružnom vlákne, os rotácie je totožná so zvislým smerom vlákna a táto os je aj osou symetrie telesa. Periodický rotačný pohyb telesa spôsobuje moment torzných síl vznikajúci skrútením pružného vlákna. Všeobecne torzné kyvadlo môže byť teleso upevnené na pružnej tyči otáčajúce sa skrúcaním tejto tyče.