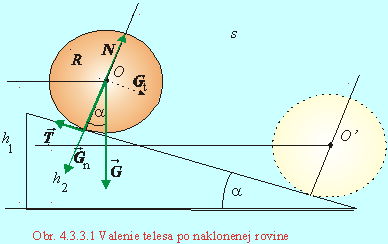
Valenie je taký pohyb telesa pozdĺž povrchu druhého telesa, pri ktorom sa obe telesá neustále dotýkajú a valiace teleso sa otáča okolo okamžitej osi danej dotykovou priamkou v povrchu druhého telesa. Dynamicky ho objasníme na pohybe rotačného telesa - valec, guľa po naklonenej rovine. Problém riešime ako rovinný pohyb v rovine preloženej zvislicou a kolmicou na naklonenú rovinu. Teleso s polomerom R má moment zotrvačnosti vzhľadom na svoju geometrickú os J*. Geometrická os je rovnobežná s dotykovou priamkou, uhol sklonu roviny je  a (Obr. 4.3.3.1). Na teleso pôsobia tieto sily: tiaž  G v ťažisku telesa, trenie T a tlaková sila od podložky N v bode dotyku telesa s podložkou. Tlaková sila je taká veľká, ako normálová zložka tiaže, ležia na jednej priamke a navzájom sa rušia. Vyjadruje to skutočnosť, že v smere kolmom na podložku je ťažisko telesa v pokoji a tento stav sa nemení.  V smere rovnobežnom s naklonenou rovinou je výsledná sila pôsobiaca na teleso.

 

 

Podľa vety o pohybe ťažiska zrýchlenie ťažiska je dané pohybovou rovnicou:

 

 

kde m je hmotnosť telesa a zrýchlenie má smer rovnobežný s naklonenou rovinou. Zrýchlenie ťažiska je konštantné, pre rýchlosť ťažiska a ním prejdenú dráhu platí:

 

 

Nepoznáme zatiaľ veľkosť sily trenia a tú môžeme určiť z druhej pohybovej rovnice. K tomu treba zvoliť vzťažný bod. Je vhodné ho voliť v dotykovom bode: V tom prípade ide o rotačný pohyb telesa okolo okamžitej osi  a platí rovnica pre rotačný pohyb

 

 

kde moment sily vzhľadom na os otáčania

 

 

J  je moment zotrvačnosti telesa vzhľadom na os otáčania a je vhodné ho vyjadriť pomocou momentu zotrvačnosti vzhľadom na rovnobežnú os prechádzajúcu ťažiskom zo Steinerovej vety:

 

 

(momenty zotrvačnosti  J* pre valec, dutý valec, guľu sme uviedli v kapitole 4.2.4).

 

Uhlové zrýchlenie telesa so zrýchlením ťažiska súvisí navzájom podľa vzťahu (Obr. 4.3.3.1):

 

 

Spätne z pohybovej rovnice ťažiska môžeme určiť silu trenia T. Valivý pohyb nastáva len v tom prípade, ak trenie je menšie ako maximálne statické trenie:

 

 

kde f je faktor statického trenia. Vidíme, že predovšetkým pre veľké uhly sklonu naklonenej roviny môže dôjsť i k čiastočnému skĺzavaniu telesa.

Úlohu možno riešiť aj ako otáčanie telesa okolo svojej geometrickej osi: potom pohybová rovnica rotačného pohybu

 

 

má tvar:

 

 

Riešenie nájdeme riešením sústavy rovníc:

 

                        

 

Ďalšou rovnicou, z ktorej môžeme určiť hľadané veličiny, napr. rýchlosť po prejdení dráhy s je zákon zachovania energie (4.2.5.6):