 Laminárne prúdenie kvapaliny v trubici kruhového prierezu
Laminárne prúdenie kvapaliny v trubici kruhového prierezu
Majme trubicu polomeru R, v ktorej laminárne prúdi kvapalina dynamickej viskozity h. Rýchlosť kvapaliny na stenách potrubia je nulová a narastá do maximálnej hodnoty v strede potrubia. Hľadáme závislosť narastania rýchlosti so vzdialenosťou od stredu trubice t.j. rýchlostný profil prúdenia v(r).
Predstavme si v prúdiacej kvapaline objem tvaru valca s polomerom r a dĺžkou l (obr.5.3.2.1)
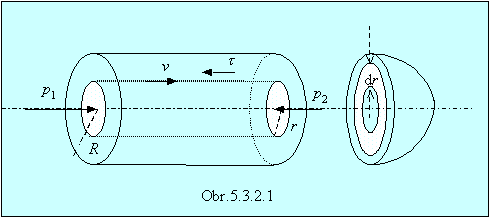
Pri stacionárnom prúdení sú rýchlosti vo všetkých bodoch konštantné (zrýchlenie a = 0), a teda aj súčet síl pôsobiacich na ľubovoľný objem kvapaliny sa musí rovnať nule. Zvoľme smer prúdenia v osi x. Pre vodorovnú trubicu je zložka objemovej tiažovej sily v smere prúdenia nulová. Musí preto platiť: Fp + Fv = 0 , kde tlaková sila Fp = Dp S = Dp p r2 a trecia sila od viskozity kvapaliny:
kde t je tangenciálne napätie úmerné dynamickej viskozite kvapaliny a gradientu rýchlosti, S* je povrch plášťa valca polomeru r a dĺžky l. Dosadením do rovnice pre rovnováhu síl
Fp i+ Fv (–i) = 0 dostaneme:
Fp i+ Fv (–i) = 0 dostaneme:
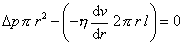 (5.3.2.1)
(5.3.2.1)Separáciou premenných a integráciou tejto rovnice:
dostaneme závislosť rýchlosti od premennej r:
Elementárny tok plôškou dS = 2p r dr je Q = v dS . Pre celkový prietok trubicou dostaneme integráciou cez celý prierez trubice Hagenov–Poisseuillov zákon:
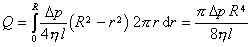 (5.3.2.4)
(5.3.2.4)Vidíme, že prietok je priamo úmerný rozdielu tlakov, nepriamo viskozite a dĺžke potrubia, ale veľmi významne (R4 !) závisí od polomeru potrubia.
Príklad 5.3.2.1
Vodorovným potrubím prúdi reálna kvapalina s dynamickou viskozitou h = 0,8 Pa×s. Meraním sa zistilo, že trubicou s priemerom d = 5 mm a dĺžkou l = 1 m pretieklo laminárnym prúdením celkove množstvo V = 0,06 ℓ za 1 minútu. Vypočítajte rozdiel tlakov na koncoch trubice a rýchlosť kvapaliny v osi trubice (obr.5.3.2.1).
Riešenie
Pre celkový prietok trubicou dostaneme z Hagenovho –Poisseuillovho zákona (5.3.2.4):
pričom
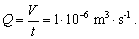
Rozdiel tlakov na koncoch trubice je:
Rýchlosť kvapaliny podľa rovnice (5.3.2.3), v osi trubice (pre r = 0), bude:
Hagenov – Poiseuillov zákon môžeme vyjadriť aj v inom tvare a to pomocou strednej rýchlosti prúdenia. Potom prietok
Po dosadení do (5.3.2.4) a úprave dostávame:
Ak vynásobíme túto rovnicu prierezom potrubia a jeho dĺžkou získame silu, ktorá spôsobuje v potrubí pohyb kvapaliny danou strednou rýchlosťou:
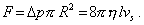 (5.3.2.5)
(5.3.2.5)Nakoľko ide o rovnovážny stav, rovnako veľký je aj trecí odpor potrubia.
Iný dôležitý vzťah odvodil Stokes pre odpor kvapaliny proti pohybu guľôčky s polomerom R. Táto sila odporu je tiež priamo úmerná rýchlosti, polomeru guľôčky a viskozite kvapaliny. Tento vzťah voláme Stokesov zákon:
FS = 6phR v (5.3.2.6)
Experimenty ukazujú, že platí iba za podmienky:
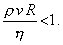
Poznámka 1
Pri turbulentnom prúdení, t.j. pri väčších rýchlostiach platí pre odpor prostredia Newtonov vzťah:
kde C je tvarový faktor, S je priečny prierez telesa.
