Tlak pod zakriveným povrchomTlak pod zakriveným povrchom

Konvexne zakrivený povrch (vypuklý) tlačí na kvapalinu viac ako konkávny povrch (dutý). Dodatočný tlak, ktorý vzniká vplyvom zakrivenia povrchu sa volá kapilárny tlak. Kapilárny tlak sa pripočíta ku kohéznemu tlaku ak je povrch vypuklý a odpočíta sa ak je povrch dutý. Výslednica molekulových síl je teda pri vypuklom povrchu väčšia. Tlak vo vnútri bubliny je preto vždy väčší, ako vonkajší tlak.
 
Určime kapilárny tlak na jednoduchom príklade guľovej kvapky s polomerom r. Práca, ktorú by vykonali povrchové sily pri zmenšení povrchu kvapky o dS vedie k zmenšeniu povrchovej energie o dE = s dS. Táto sa musí rovnať práci na zmenšenie objemu o dV pri kapilárnom tlaku pk:  dW = pk dV.  Pre diferenciály povrchu a objemu gule platí:
 
dS = 8 p r dr a dV= 4 p r2 dr.
 
Potom   
 
 
a  pre  kapilárny tlak dostávame:
 
        (5.3.4.1)
 
V bubline vytvorenej napríklad z mydlového roztoku sú zakrivené povrchy dva, a tlak v mydlovej bubline je väčší ako vonkajší tlak o dvojnásobok pk. Tlak v bubline:
 
        (5.3.4.2)
 
Vo všeobecnosti môžeme zakrivený tvar povrchu charakterizovať pomocou polomerov kružníc r1 a r2 vyjadrujúcich zakrivenie povrchu v dvoch na seba kolmých rezoch. Pre kapilárny tlak potom platí Laplaceov vzťah:
 
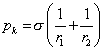        (5.3.4.3)
 
Povrch je prakticky vždy rozhranie medzi dvomi prostrediami, napríklad kvapalina - plyn, alebo kvapalina - para. Na rozhraní troch prostredí, ktoré vznikne napríklad vtedy, keď kvapneme kvapku parafínového oleja na vodu, sa prejavia tri rozhrania a teda aj tri tangenciálne povrchové napätia  (obr.5.3.4.1).
 

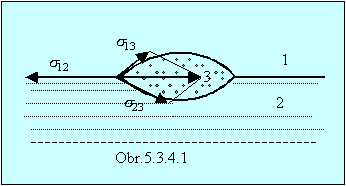
Sú to napätia medzi vodou a vzduchom σ12, vodou a  olejom σ23 a olejom a vzduchom σ13 . Ak sú rozhrania voľne pohyblivé, povrchy nadobudnú tvar, pri ktorom výslednica všetkých troch povrchových napätí bude nulová. Kvapka môže zostať kvapkou len ak: σ12 < σ13 + σ23. V prípade, že σ12 > σ13 + σ23, olej sa roztiahne po povrchu kvapaliny v takmer monomolekulovej vrstve. Také vlastnosti na styku s vodou má napríklad olivový olej. Tenké olejové vrstvy môžeme vidieť aj po daždi, na olejom znečistenej ceste. Ak kvapalina hraničí s pevnou stenou, je povrch kvapaliny na styku so stenou vo všeobecnosti zdvihnutý, (kvapalina povrch zmáča), alebo stlačený. Uhol, ktorý zviera dotyčnica k povrchu kvapaliny so stenou nádoby je krajný uhol. (obr.5.3.4.2). Za rovnováhy platí σ13 = σ12  +  σ23 cosu. Krajný uhol bude ostrý, ak σ13 – σ12  > 0 a tupý  ak σ13 – σ12  < 0.
 
 
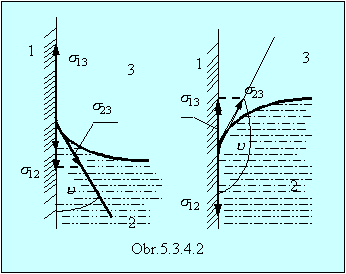
Pri ponorení úzkej trubice do kvapaliny sa vytvorí zakrivený povrch kvapaliny v trubici (Obr.5.3.4.3). Podľa toho, či kvapalina zmáča steny trubice, alebo nie, bude zakrivený povrch dutý, alebo vypuklý. Ak  kvapalina  zmáča  steny trubice vzniká kapilárne zvýšenie – kapilárna elevácia. Tlak pod dutým zakriveným povrchom bude totiž menší o
 
 
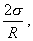
kde R je polomer krivosti vzniknutého menisku v kapiláre.
 

 
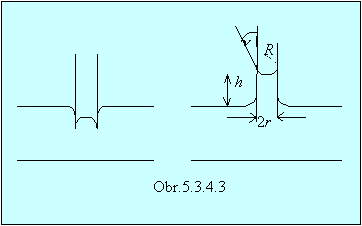
Prevaha vonkajšieho tlaku potom vytláča kvapalinu v kapiláre nahor a to  dovtedy,  kým sa zníženie tlaku nebude rovnať hydrostatickému tlaku zdvihnutej kvapaliny. Pre výšku stĺpca kvapaliny - tzv. elevačnú výšku, potom platí:
 
        (5.3.4.4)
 
Kapilárna elevácia poskytuje takto jednoduchú metódu na určenie povrchového napätia.
 
Opačný jav je kapilárna depresia. Dochádza k nej vtedy, keď sa kvapalina snaží zo steny kapiláry stiahnuť. Povrch kvapaliny bude vypuklý a tlak v kvapaline o kapilárny tlak väčší. Hladina kvapaliny v kapiláre poklesne.
 
 
Príklad 5.3.4.1

Do vody sú ponorené dve sklené kapiláry s polomermi r1 = 1 mm, r2 = 1,5 mm. Vypočítajte povrchové napätie, keď rozdiel hladiny vodných stĺpcov v týchto kapilárach je 4,9 mm a keď predpokladáme, že voda dokonale zmáča steny sklenej trubice.

Riešenie
Kapilárna elevácia vody v kapiláre vytlačí stĺpec vody do výšky
 
 
 
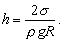
Polomer zakrivenia kvapaliny v kapiláre môžeme vyjadriť:
 
 
 
kde r je polomer kapiláry, υ je krajný uhol  (obr.5.3.4.3) - teda uhol, ktorý zviera voda so stenou kapiláry, ρ je hustota vody. Ak voda dokonale zmáča stenu, bude R = r . Rozdiel výšok hladín pri dvoch rôznych kapilárach s polomermi r1a r2 bude:
 
 
 
Odtiaľ dostaneme pre povrchové napätie:
 
 
 

Kontrolné otázky

  1. Ak položíme kúsok cukru alebo kriedy na mokrú špongiu zvlhnú, ale keď položíme mokrú kriedu na suchú špongiu ostane suchá. Prečo?
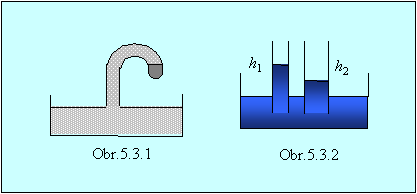
  2. Do vody je ponorená zahnutá kapilárna trubička (obr.5.3.1). Môže voda po jej vystúpení do kapiláry odkvapkávať naspäť do nádoby a vytvoriť tak “večný kolobeh"?

  3. Dve kapiláry rôzneho priemeru sú ponorené do nádoby s vodou a voda v nich vystúpi do výšok h1, resp. h2 (obr.5.3.2). Zmení sa pomer hladín vody v kapilárach pri zahrievaní vody?
  4. Polomer kapilár  kapilárnej sústavy rastlín je 0,001 cm. Povrchové napätie vody (pri 20 °C) je 0,072 N×m–1. Do akej výšky kapilár môže vystúpiť voda pôsobením síl povrchového napätia?
  5. V dvoch kapilárach s polomermi 0,5 mm a 2 mm, ponorených do nádoby s ortuťou, je rozdiel hladín ortuti 10,5 mm. Aké je povrchové napätie ortuti?
  6. Prečo je výhodnejšie pri člnkovaní v smere prúdu rieky člnkovať v strede rieky a naopak pridŕžať sa brehov keď člnkujeme proti prúdu?
  7. Prečo lietadlá štartujú a pristávajú podľa možnosti proti smeru vetra?
  8. Dve rovnaké olovené guľôčky pustíme do dvoch rovnakých nádob s vodou. V jednej nádobe je ale studená voda 10°C, a v druhej má voda teplotu 40°C. V ktorej nádobe guľôčka skôr dopadne na dno a prečo?
  9. Stredná rýchlosť krvi v aorte (polomer r » 1 cm) je  » 30 cm.s–1. Je prúdenie krvi laminárne, alebo turbulentné?
 

Príklady

1.      Potrubím pretečie Q = 200 cm3×s–1 vody, ktorá má v podmienkach pokusu dynamickú viskozitu   h = 0,001 Pa×s. Akú podmienku musí spĺňať priemer potrubia, aby prúdenie bolo laminárne? (d > 11 cm)
 
2.      Oceľová guľôčka s priemerom 1 mm padá konštantnou rýchlosťou v = 0,185 cm×s–1 vo veľkej nádobe naplnenej olejom hustoty r = 900 kg×m–3. Určte dynamickú viskozitu oleja! (2 Pa×s)
 
3.      Akú najväčšiu rýchlosť môže získať dažďová kvapka priemeru  d = 0,3 mm vo vzduchu? (2,7 m×s-1)
 
4.      Kvapôčka hmly padá vo vzduchu rovnomerne rýchlosťou 1 m×s–1. Aká veľká je kvapka, ak odpor vzduchu je podľa Stokesovho zákona F = 6phrv ? Vztlakovú silu zanedbajte! (9,1×10-5 m)
 
5.        Aká je kapilárna depresia ortuti v sklenej rúrke polomeru  r = 1 mm, keď povrchové napätie ortuti je σ = 0,433 N×m-1 a keď krajný uhol (uhol, ktorý zviera rozhranie ortuť-vzduch so sklenou stenou) υ  = 120°, rHg = 13,6×103 kg×m–3? (3,2 mm)