Kmity sústavy dvoch hmotných bodov
Často sa stretávame s dvojčasticovými kmitajúcimi sústavami, v ktorých ani jednu z častíc nemôžeme považovať za nepohyblivú. Jednoduchým príkladom sú dvojatómové molekuly, napr. H2, HCl, CO, FH, atď. Predstavme si takúto sústavu pomocou pružiny a dvoch hmotností m1a m2 ako je zobrazená na obr.6.1.4.
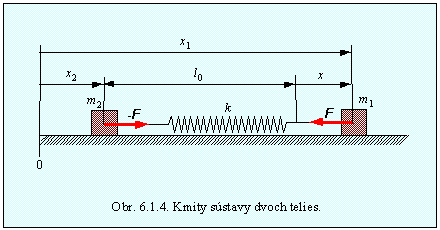
Pre jednotlivé hmotnosti platia pohybové rovnice
(6.1.4.1)
(6.1.4.2)kde x1 a x2 sú súradnice hmotností m1a m2 a x = x1 – x2 – l0 je predĺženie pružiny, pričom l0 je pôvodná (rovnovážna) dĺžka pružiny. Vynásobme rovnice (6.1.4.1) a (6.1.4.2) postupne hmotnosťami m2 a m1 a odčítajme ich. Dostávame rovnicu
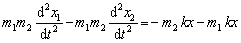(6.1.4.3)ktorú môžeme upraviť do tvaru
(6.1.4.4)odkiaľ po využití d(x1– x2 ) = d(x + l0) = dx (pozn.: l0 je konštanta) dostávame
(6.1.4.5)kde
(6.1.4.6)To je však rovnica harmonického oscilátora (viď 6.1.2.2) s hmotnosťou µr, ktorú voláme redukovaná hmotnosť. Vidíme, že kmity sústavy dvoch hmotných bodov môžeme skúmať ako kmity jednoduchého harmonického oscilátora s tou istou silovou konštantou, ale redukovanou hmotnosťou. Uhlová frekvencia kmitov takejto sústavy je
Príklad 6.1.5
Molekula CO kmitá s frekvenciou f = 2.1013 s–1. Vypočítajte silovú konštantu väzby molekuly CO, keď hmotnosti atómov uhlíka a kyslíka sú mC = 1,990.10–26 kg, m0 =2,655.10–26 kg.
Riešenie
Umiestnenie atómov kyslíka a uhlíka v súradnej sústave je znázornené na obr. 6.1.5. V stave pokoja platí : x2 – x1 = lo, kde lo je vzájomná vzdialenosť atómov C, O.
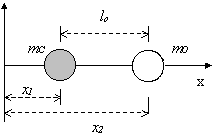
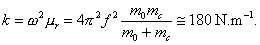
Pri kmitaní molekuly bude sila, ktorou pôsobí molekulová väzba na jednotlivé atómy závisieť od zmeny dĺžky väzby: x = x2 – x1 – lo a bude pre oba atómy čo do veľkosti rovnaká, ale opačného smeru. Návratné sily budú mať vždy smer do rovnovážnej polohy. Platia rovnice (6.1.4.1- 6.1.4.6) uvedené v predchádzajúcom štúdiu kmitajúcej sústavy dvoch hmotných bodov. Po úpravách totožných s predchádzajúcim odvodením a zavedení redukovanej hmotnosti pre hľadanú silovú konštantu väzby molekuly CO dostaneme:
