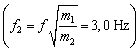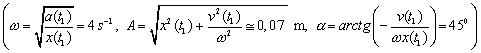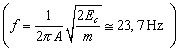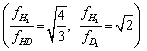Vektorové zobrazenie harmonického kmitavého pohybu
Vektorové zobrazenie harmonického kmitavého pohybu
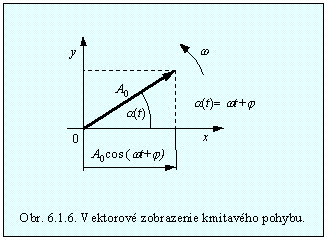
Mnohé úlohy, hlavne skladanie kmitov, sa značne zjednodušia, ak kmitavý pohyb zobrazíme priemetom koncového bodu rotujúceho vektora. Podľa Obr. 6.1.6 zvoľme na priamke x počiatočný bod a umiestnime v ňom počiatok vektora otáčajúceho sa uhlovou rýchlosťou w v naznačenom smere. Nech veľkosť vektora je A0 a nech uhol, ktorý rotujúci vektor zvieral s osou x v čase t = 0 je j . Potom priemet vektora do priamky x sa rovná práve A0cos(wt+j), čo je výraz pre časovú závislosť výchylky pri harmonickom kmitavom pohybe. Vektorové zobrazenie sa dá výhodne použiť pri skladaní kmitov.
Kontrolné otázky
-
Ktoré fyzikálne javy voláme kmity?
-
Čo je rovnovážna poloha?
-
Aký význam má amplitúda a čo je fáza kmitu?
-
Ako sa mení s časom amplitúda netlmeného kmitavého pohybu?
-
V ktorom bode má teleso vykonávajúce harmonický kmitavý pohyb po priamke maximálne zrýchlenie a v ktorom bode maximálnu rýchlosť?
-
Akou funkciou amplitúdy je energia netlmeného harmonického pohybu?
-
Ak častica vykonáva harmonické kmity s amplitúdou A, akú vzdialenosť prejde za jednu periódu?
-
V ktorom bode má teleso konajúce netlmené harmonické kmity maximálnu rýchlosť a v ktorom bode má rýchlosť nulovú?
-
V ktorom bode má teleso konajúce netlmené harmonické kmity maximálne zrýchlenie a v ktorom bode má zrýchlenie nulové?
-
V ktorom bode má teleso konajúce netlmené harmonické kmity maximálnu kinetickú energiu a v ktorom maximálnu potenciálnu energiu?
-
Aká je tuhosť pružiny (silová konštanta), ak pri zavesení hmotnosti 0,3 kg na pružinu sa pružina predĺži o 0,15 m?
-
Aká je silová konštanta pružiny harmonického oscilátora, ak amplitúda kmitov je 0,1 m a celková energia tohto harmonického oscilátora je 0,098 J?
-
Ak zdvojnásobíme amplitúdu kmitov netlmeného harmonického oscilátora, ako sa zmení maximálna rýchlosť a celková mechanická energia?
-
Energia kmitov jedného harmonického oscilátora je 10-krát väčšia ako druhého a silová konštanta prvého systému je dvakrát väčšia ako druhého. Čo môžete povedať o amplitúdach kmitov týchto sústav?
-
Guľka zavesená na pružine koná netlmený harmonický pohyb s periódou 0,5 s. Aká je frekvencia kmitov?
-
Teleso koná netlmený harmonický pohyb s amplitúdou A = 3 m, frekvenciou f = 4 Hz a v čase t = 0 s sa nachádza vo vzdialenosti 1,5 m od rovnovážnej polohy. Napíšte výraz pre okamžitú výchylku telesa.
Príklady
6.1.6 Gumový záves má celkovú dĺžku 45 cm ak je na ňom zavesené závažie hmotnosti 1,8 kg. Ak naň zavesíme závažie hmotnosti 2,5 kg, bude dĺžka závesu 68 cm. Aká je tuhosť takejto gumovej pružiny? Predpokladajte, že deformácia je priamo úmerná pôsobiacej sile.
6.1.7 Ak je na pružine zavesená hmotnosť 0,8 kg, kmitá s frekvenciou 2,4 Hz. Aká bude frekvencia kmitov, ak na pružinu zavesíme záťaž hmotnosti 0,5 kg?6.1.8 Výchylka harmonického oscilátora v závislosti od času je x(t) = 2 cos [(5/4) p t + p/6] m. Aká je perióda a frekvencia kmitov? Aká je výchylka a rýchlosť kmitavého pohybu v čase t = 0 s ?
6.1.9 Netlmený harmonický oscilátor má v určitom čase t1 okamžitú výchylku x(t1) = 5 cm, rýchlosť v(t1) = 0,2 m.s–1 a zrýchlenie a(t1) = – 0,8 m.s–2. Aká je amplitúda A, uhlová frekvencia w a fázová konštanta tohto pohybu ?
6.1.10 Vypočítajte frekvenciu netlmeného harmonického pohybu hmotného bodu s hmotnosťou m = 1 g, keď amplitúda pohybu A = 0,3 m a celková energia hmotného bodu pri tomto pohybe je EC = 1 J.
6.1.11 Akú časť celkovej energie harmonického oscilátora tvorí kinetická a akú potenciálna energia, keď výchylka sa rovná polovici amplitúdy? (Ep = 25%, Ek= 75%)6.1.12 Na natiahnutie pružiny o vzdialenosť y = 5 cm je potrebná práca W = 25 mJ. Vypočítajte, s akou periódou bude kmitať teleso s hmotnosťou m = 100 g zavesené na tejto pružine.
6.1.13 Silová konštanta väzby v molekulách, v ktorých je vodík nahradený deutériom sa nezmení oproti pôvodnej molekule. Odlišné sú však frekvencie vibrácií takýchto väzieb. Určte, aký je pomer vibračných frekvencií harmonických kmitov molekúl H2, HD a D2, ak kmitajú ako harmonické oscilátory. Hmotnosť atómu deutéria je dvakrát väčšia ako hmotnosť atómu vodíka.