Najjednoduchším a najnázornejším príkladom vlnenia je lineárna harmonická priečna vlna. Experimentálne ju vytvoríme napríklad rozkmitaním napnutého pružného vlákna, alebo gumovej hadice. Predpokladáme, že je naše napnuté vlákno dostatočne dlhé, aby sme sa vyhli komplikáciám, ktoré by boli spôsobené odrazom vlnenia na jeho konci. Je to vlákno, ktoré je napnuté, na jednom jeho konci je zdroj kmitania, ale na druhom konci ako by nebolo ohraničené.

Hľadáme matematickú funkciu, ktorá bude popisovať postupujúcu vlnu. Nech je vlákno orientované v smere osi x a v počiatku súradníc máme harmonický zdroj kmitov. Hľadaná funkcia bude funkciou premenných x a t. Nech výchylka v počiatku je daná harmonickou funkciou

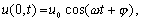        (6.2.2.1)

kde u0 je amplitúda kmitov, w je kruhová frekvencia kmitov a j je fázová konštanta. Tento harmonický „rozruch“ sa bude šíriť pružným prostredím určitou rýchlosťou v a do bodu so súradnicou x príde o čas t = x/v  neskôr. Výchylka v bode vzdialenom od zdroja kmitov o x bude

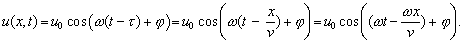        (6.2.2.2)

Tento zápis môžeme ďalej upraviť do názornejšieho tvaru, ak využijeme, že w = 2p/T a zavedieme novú veličinu – vlnovú dĺžku. Vlnová dĺžka je vzdialenosť, ktorú prejde fáza vlny za jednu periódu.

l = v T.        (6.2.2.3)

Na obr. 6.2.1  je zobrazená vlna v určitom časovom okamžiku. Vidíme, že vlnová dĺžka je najmenšia vzdialenosť bodov prostredia, ktorých výchylka má rovnakú fázu.

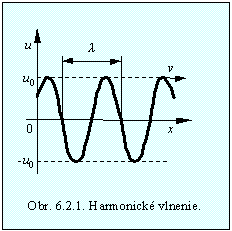
Je užitočné definovať   uhlové vlnové číslo  (používa sa tiež názov vlnové číslo)

k = 2p/l.        (6.2.2.4)

Jednotkou uhlového vlnového čísla v sústave SI je radián m–1.

Položme, kvôli jednoduchosti, fázovú konštantu j = 0 a vlnovú funkciu vyjadríme v najčastejšie používaných tvaroch

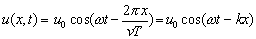        (6.2.2.5)

Vlnová funkcia určuje výchylku elementu prostredia vzdialeného od zdroja o vzdialenosť x v čase t. Výchylka postupuje v smere narastania x, teda zľava do prava. Elementy prostredia však nepostupujú, ale iba oscilujú okolo rovnovážnej polohy a to ako pri vlnení priečnom, tak aj pri pozdĺžnom. Rýchlosť postupu výchylky v smere šírenia sa vlnenia je daná konštantnou hodnotou fázy vlnovej funkcie. Fáza je rovnaká ak wt – kx sa rovná určitej konštante. Zoberme maximálnu výchylku a položme wt – kx = 0. Potom dostávame

        (6.2.2.6)

Pri formulovaní rovnice (6.2.2.2) sme zaviedli rýchlosť postupu vlnenia. Ak si uvedomíme ako sme definovali vlnové číslo, vidíme, že fázová rýchlosť je rýchlosť šírenia sa fázy vlny v smere šírenia vlnenia. Rýchlosť, ktorú sme použili pri formulovaní rovnice (6.2.2.2), je práve fázová rýchlosť. Iná rýchlosť je rýchlosť oscilácie elementov prostredia. Je určená časovou deriváciou výchylky, teda

        (6.2.2.7)

Vlnová funkcia harmonickej vlny je periodická funkcia času aj súradnice. Pre fixovanú hodnotu x, je to periodická funkcia času, pre určitý časový okamih t je to periodická funkcia súradnice.

O vlnení sme doposiaľ predpokladali, že sa šíri v smere narastania súradnice x, teda v kladnom smere osi x. V prípade, že vlnenie bude postupovať opačným smerom, potom bod v mieste  x >0 bude mať určitú výchylku o časový interval t = x/v skôr ako bod x = 0. Vlnová funkcia pre vlnenie postupujúce v opačnom smere, teda sprava doľava, sa bude líšiť znamienkom a je určená funkciou

        (6.2.2.8)

Toto vyjadrenie vlnovej funkcie vyhovuje pozdĺžnemu vlneniu aj priečnemu vlneniu. Na úplné určenie vlnenia v prípade priečneho vlnenia je ešte potrebné určiť smer kmitania.

Vlnová funkcia nemusí byť vo všeobecnosti harmonická funkcia. Ak zdroj vlnenia umiestnený v začiatku súradnicovej sústavy kmitá vo všeobecnosti podľa rovnice
u = f(t), potom vlnová funkcia vlnenia je funkcia typu

        (6.2.2.9)

Znamienko mínus platí pre vlnu postupujúcu v kladnom smere osi x, znamienko plus pre vlnu postupujúcu v zápornom smere osi x.

Pri šírení vlnenia v priestore vlnová funkcia bude funkciou premenných x, y, z a času t. Množina bodov kmitajúcich s rovnakou fázou nazýva vlnoplocha. Vlnoplochy môžu mať rôzny tvar, najjednoduchší tvar vlnoplochy je rovina, alebo guľová plocha. Ak sa rovinná vlna šíri napríklad v smere osi x, potom pre dané x body s ľubovoľnou hodnotou súradnice y, resp. z budú mať rovnakú fázu.

Vlnovú funkciu rovinnej vlny šíriacej sa v priestore vyjadruje rovnica

        (6.2.2.10)

v ktorej r je polohový vektor daného bodu a k je uhlový vlnový vektor ( tiež iba vlnový vektor).

Veľkosť uhlového vlnového vektora sa rovná uhlovému vlnovému číslu  |k| =  k = 2p/l.

Vo vzduchu sa šíri harmonické zvukové vlnenie s frekvenciou f = 2 kHz a amplitúdou A = 1 mm. Rýchlosť zvuku vo vzduchu je n = 340 ms –1. Určte vlnovú dĺžku vlnenia a maximálnu rýchlosť molekúl vzduchu.

Výchylku molekúl z rovnovážnej polohy vyjadruje vlnová funkcia u = Acos (w t – kx + j). Pre rýchlosť zvuku (fázovú rýchlosť) platí

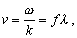
odkiaľ pre vlnovú dĺžku dostávame

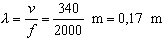
Rýchlosť kmitajúcich molekúl je

Maximálna rýchlosť molekúl je maximálna hodnota tejto funkcie, t. j.

Určte tvar vlnoplochy vlnenia vyjadreného vlnovou funkciou u(t,x) = A cos(wt – kx).

Vlnoplocha je množina bodov, ktoré majú v danom okamihu   t = t1   rovnakú fázu. Označme túto fázu   j = j1 . Potom   wt1 – kx =j1  z  čoho

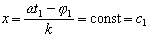
Vlnoplocha je množina bodov, ktoré v čase t1 majú x = c1. Množina takých bodov tvorí rovinu kolmú na os  x  a pretínajúcu túto os v bode   x = c1.