Celkom všeobecný opis šírenia vlnenia v priestore a čase obsahuje vlnová rovnica. Vlnová rovnica je parciálna diferenciálna rovnica tvaru

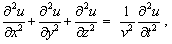        (6.2.3.1)

v ktorej u je symbol pre výchylku a n je fázová rýchlosť šírenia vlnenia. Ak sa vlnenie šíri iba v jednom smere, napr. v smere osi x, potom vlnová rovnica má tvar

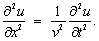        (6.2.3.2)

Riešením vlnovej rovnice sú vlnové funkcie, t.j. funkcie typu  f(x, t,) = f(t ± x/n). Ponechávame na čitateľa, aby sa presvedčil, že vlnová funkcia (6.2.2.5) aj (6.2.2.8) je riešením rovnice (6.2.3.2), resp. (6.2.2.10) je riešením vlnovej rovnice (6.2.3.1).

Na rozdiel od vlnovej funkcie, ktorá predstavuje iba kinematický popis vlnenia, vlnová rovnica zahrňuje i dynamiku prostredia, resp. z nej vyplýva. Súvislosť medzi pôsobiacimi silami a vlastnosťami určitého prostredia  sa prejaví vo výraze pre rýchlosť  v. Vlnová rovnica má rovnaký tvar pre priečne aj pozdĺžne vlnenie. Pri priečnom vlnení je ešte potrebné zadať rovinu kmitov. Aby sme boli konkrétni nájdime vlnovú rovnicu pre kmity struny napínanej silou F, a ktorej hmotnosť na jednotku dĺžky je  m = m/l, kde l je dĺžka struny a ktorej kmity prebiehajú v smere osi y.

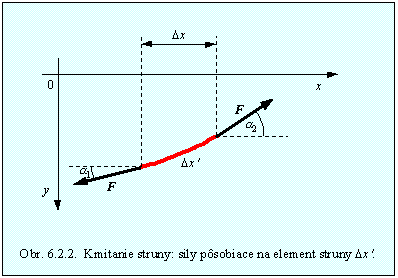
Vyberme si element tejto struny Dx´ v ktorého koncoch zvierajú dotyčnice ku strune malé uhly a₁ a a₂ (obr.6.2.2 ) . Pod malými rozumieme uhly, pre ktoré platí a@ sina @ tga = dy/dx. Pri malých uhloch tiež platí Dx´ = Dx, kde  Dx je priemet elementu struny Dx´ do osi  x.

Na vybraný element Dx´ v smere osi y pôsobí sila veľkosti

F_y = Fsina₁ – Fsina₂ @ Fa₁ – Fa₂ = F Da

Pre túto silu má pohybová rovnica v smere osi y tvar

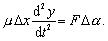        (6.2.3.3)

Úpravou dostávame

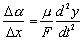        (6.2.3.4)

a po prechode k nekonečne malým elementom  dx

        (6.2.3.5)

Ak do tejto rovnice dosadíme   a = dy/dx dostávame vlnovú rovnicu struny

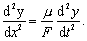        (6.2.3.6)

Porovnaním s vlnovou rovnicou (6.2.3.2) dostávame pre rýchlosť šírenia vlnenia v strune vzťah

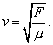        (6.2.3.7)

Analýzou pohybového stavu elementu napnutej struny sme získali vlnovú rovnicu pre priečne vlnenie šíriace sa po strune. Štúdiom pohybu elementov vzduchu môžeme získať vzťah pre rýchlosť šírenia vlnenia v plyne

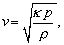        (6.2.3.8)

kde k je Poissonova konštanta a r je hustota plynu. V pružnej tyči sa pozdĺžna vlna šíri rýchlosťou

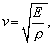        (6.2.3.9)

kde E je Youngov modul pružnosti.

Ukážte, že funkcia u(t,x) = A cos(wt – kx) je riešením jednorozmernej i trojrozmernej vlnovej rovnice. Určte fázovú rýchlosť tohto vlnenia.

Jednorozmerná vlnová rovnica je

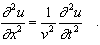
Ľavá strana je v našom prípade

Pravá strana je

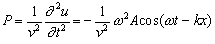
Podľa vlnovej rovnice by malo platiť L = P. Po dosadení a porovnaní dostávame, že daná funkcia je riešením jednorozmernej vlnovej funkcie, pričom fázovú rýchlosť vlnenia určuje

n =  w / k.

Trojrozmerná vlnová rovnica je

Derivácie na ľavej strane sú 

                

takže dostávame rovnakú rovnicu a rovnakú fázovú rýchlosť ako v jednorozmernom prípade.

Po voľne visiacom lane dĺžky  l a hmotnosti  m sa šíri vlnenie Obr.(6.2.3). Určite (a) rýchlosť šírenia priečneho vlnenia po lane ako funkciu polohy bodu na lane, (b) čas, za ktorý krátky priečny rozruch prejde celým lanom.

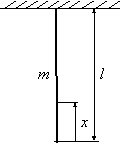
a)        Rýchlosť šírenia vlnenia je

b)        Pre rýchlosť šírenia možno písať 

n = dx/dt.