Stojaté vlnenie je jav, ktorý vzniká vtedy, keď sa skladajú dve vlnenia s rovnakou amplitúdou a frekvenciou postupujúce proti sebe.  Majme dve lineárne polarizované harmonické vlny rovnakej frekvencie, amplitúdy a postupujúce proti sebe v osi x. Začiatok súradníc si zvoľme v bode v ktorom sa obidve vlny stretajú s rovnakou fázou. Vlneniam odpovedajú vlnové funkcie

        (6.2.5.2.1)

        (6.2.5.2.2)

Podľa princípu superpozície výsledné vlnenie bude určené funkciou

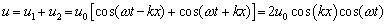        (6.2.5.2.3)

Vlnová funkcia sa rozpadla na súčin dvoch harmonických funkcií. Nemá tvar 6.2.2.9, preto nepopisuje postupujúce vlnenie, ale, ako uvidíme ďalej, tzv. stojaté vlnenie.

V tomto vyjadrení stavu, ktorý vznikol interferenciou proti sebe postupujúcich vlnení, amplitúdu výsledného vlnenia určuje funkcia   |2u_ocos kx|. Amplitúda závisí od polohy kmitajúceho bodu.  Výsledné vlnenie bude mať nulovú amplitúdu v miestach, v ktorých cos kx = 0, t.j. vo všetkých bodoch, pre ktoré platí     kx = (2n + 1) p/2, alebo po dosadení za k =  2p/l sú to miesta, pre ktoré platí

        (6.2.5.2.4)

Tieto miesta nazývame uzly. Vzdialenosť dvoch susedných uzlov je

        (6.2.5.2.5)

teda polovica vlnovej dĺžky. S maximálnou výchylkou budú kmitať body, v ktorých cos kx = ±1. Pre tieto miesta  kx =  np, alebo

        (6.2.5.2.6)

Tieto miesta nazývame kmitne. Vzdialenosť dvoch susedných kmitní

        (6.2.5.2.7)

a tiež sa rovná polovici vlnovej dĺžky.

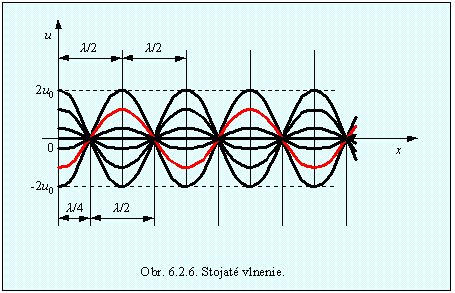
Na rozdiel od postupujúceho vlnenia, pri ktorom všetky body prostredia kmitajú s rovnakou amplitúdou ale s rôznou fázou, pri stojatom vlnení je fáza kmitov všetkých bodov prostredia medzi dvoma uzlami rovnaká a pri prechode uzlom sa mení na opačnú. Každý bod prostredia však kmitá  s určitou amplitúdou, ktorá závisí od jeho polohy a je určená funkciou 2u_o| cos kx | . V uzloch sú výchylky vždy nulové, v kmitniach vždy maximálne. V určitom čase, keď cos w t  v  (6.2.5.2.3) sa rovná nule, je výchylka všetkých bodov prostredia nulová. Ak cos w t = ±1, majú všetky body svoje maximálne výchylky, ktorých amplitúda sa rovná  2 u_o| cos kx | . Priebeh stojatého vlnenia je na obr.  6.2.6.

Stojaté vlnenie vznikne, ak ohraničený rad bodov, pružné vlákno, strunu rozkmitáme na obidvoch koncoch, alebo ak rozkmitáme jeden jej koniec a druhý je upevnený. Na upevnenom konci nastane odraz vlnenia a odrazená vlna  postupuje proti pôvodnej vlne a s ňou interferuje.

Pri odraze vlnenia rozlišujeme odraz na voľnom konci a odraz na pevnom konci. Pri odraze na voľnom konci je v mieste odrazu kmitňa a vlnenie sa odráža na voľnom konci s rovnakou fázou. Pri odraze na pevnom konci je v mieste odrazu uzol a vlnenie sa odráža s opačnou fázou.

Pri stojatom vlnení nemáme postupujúce čelo vlny, ako pri vlne šíriacej sa napr. po pružnom vlákne. Niekedy sa preto tiež používa možno výstižnejší termín pre stojaté vlnenie a to „chvenie“. V ohraničenom prostredí, ktorým je napr. napnutá husľová struna nemôže vzniknúť stojaté vlnenie ľubovoľnej frekvencie. Rýchlosť šírenia sa vlnenia je určená vlastnosťami struny a jej napnutím vzťahom (6.2.3.7). Možné budú iba také vlnové dĺžky a teda aj frekvencie, pre ktoré sú na koncoch struny uzly. Dĺžka struny sa preto musí rovnať násobku l / 2.

Stojaté vlnenie vzniklo interferenciou dvoch proti sebe postupujúcich vlnení s frekvenciou f = 475 Hz.  Vzdialenosť susedných uzlov bola   d = 1,5 m.  Určte rýchlosť postupu vlnenia v danom prostredí.

Vzdialenosť susedných uzlov stojatého vlnenia sa rovná polovici vlnovej dĺžky vlnení, ktorých interferenciou stojaté vlnenie vzniklo. Preto d = l/2 ,  z čoho l = 2d.  Rýchlosť postupu vlnenia je   v = f l = f 2 d =475.2.1,5 m.s^-1 = 1425 m.s^-1.

Po strune sa proti sebe z dvoch zdrojov šíria rovnakou rýchlosťou n dve harmonické vlnenia a vzájomne interferujú. Zdroje majú rovnakú amplitúdu A,  rovnakú uhlovú frekvenciu  w  a kmitajú vo fáze. Prvý zdroj je umiestnený v počiatku súradnicovej sústavy  x = 0, jeho kmitanie vyjadruje funkcia kosínus s fázovou konštantou  j₁ .  Druhý zdroj sa nachádza v polohe  x = d ,  kde  d > 0 .

     (a) Nájdite vlnovú funkciu pohybu struny v oblasti medzi zdrojmi.

     (b) Určte polohy kmitní a uzlov.

(a)  Vlnové rovnice interferujúcich vlnení sú:

Zdroje sú stále vo fáze, ich výchylky sú v každom okamihu rovnaké, takže platí u₁(t,0) = u₂(t,0). Pre argumenty vlnových funkcií potom

kde  n  je ľubovoľné celé číslo,  ktoré môžeme zvoliť rovné nule  a  j₂ = – kd + j₁ .Vlnové rovnice interferujúcich vlnení sú teda:

Vlnová funkcia výsledného vlnenia, ktoré vzniká ich skladaním, je  u = u₁ + u₂ .

S využitím známeho trigonometrického vzťahu

   

dostávame

čo je vlnová funkcia stojatého vlnenia s polohovo závislou amplitúdou

Zo vzťahu pre fázovú rýchlosť  n= w/k môžeme v týchto výrazoch nahradiť uhlové vlnové číslo  k výrazom    k =  w/n   čím dostávame

a

Kmitne sú miesta s najväčšou amplitúdou  A_výsl(x) ,  čomu zodpovedá argument funkcie kosínus

kde  n  je celé číslo. Z tejto podmienky vyplýva, že

Kmitne sú všetky body vyhovujúce tejto podmienke a súčasne podmienke  0 £ x £ d, ktorá vystihuje fakt, že stojaté vlnenie vzniká iba v oblasti medzi zdrojmi.

Uzly sú miesta s nulovou amplitúdou  a A_výsl(x) = 0. Funkcia kosínus bude nulová ak

pričom súčasne musí platiť  0 £ x £ d .               

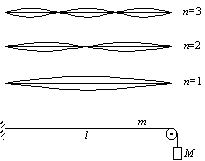
Vodorovný pružný drôt má jeden koniec pevný. Druhý koniec prechádza pevnou kladkou a je na ňom tesne pod kladkou zavesené závažie s hmotnosťou  M = 5 kg.  Vzdialenosť medzi pevným koncom a kladkou je  l = 3 m,  hmotnosť tohto úseku drôtu je  m = 100 g.  Určte možné frekvencie kmitania drôtu.

Na drôte sa môže ustáliť iba také kmitanie (stojaté vlnenie), ktoré má na pevných koncoch drôtu uzly(obr. 6.2.7).

Z  obr.6.2.7  pre možné vlnové dĺžky vyplýva podmienka l = n l /2 , kde  n  je celé číslo. Vlnová dĺžka súvisí s frekvenciou podľa vzťahu n= lf,  kde fázová rýchlosť  n je určená napínacou silou  F = Mg  a dĺžkovou hustotou struny  s = m/l.

Platí

   

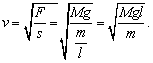
Preto     

odkiaľ

Dosadením do rovnice  pre možné vlnové dĺžky dostávame podmienku

z ktorej pre možné frekvencie kmitania drôtu vyplýva

Základná frekvencia (pre  n = 1 ) je  f₁ = 6,39 Hz,  vyššie harmonické (pre  n = 2, 3,...) sú  f₂ = 12,8Hz,  f₃ = 19,2 Hz ,...