Ak chceme na napnutej strune vyvolať vlnenie, musíme napnutú strunu vychýliť. Pri vychýlení strunu deformujeme a musíme na to vynaložiť prácu, ktorá sa rovná energii pružnej deformácie. Podobne to bolo pri harmonickom oscilátore, keď sme natiahnutím pružiny dodali sústave energiu v podobe potenciálnej energie deformovanej pružiny. Ak chceme na pružnej tyči vytvoriť pozdĺžne vlnenie, tak napr. úderom kladiva na jeden koniec tyče vytvoríme pružnú deformáciu okrajových elementov tyče, ktorá sa bude ďalej šíriť pružným prostredím. Vlna šíriaca sa prostredím prenáša takto kinetickú aj potenciálnu energiu jedného elementu tyče na ďalšie.

 

Hľadáme strednú mechanickú energiu objemovej jednotky prostredia hustoty r, ktorým sa šíri harmonické vlnenie s uhlovou frekvenciou w a amplitúdou u_o. Kmitajúce elementy prostredia budú mať kinetickú energiu a tiež potenciálnu energiu spôsobenú deformáciou. Objemová hustota kinetickej energie v bode so súradnicou x je

 

        (6.2.6.1)

 

Stredná hodnota hustoty kinetickej energie

 

        (6.2.6.2)

 

Pri harmonickom oscilátore sme si ukázali (príklad 6.1.4), že stredná hodnota kinetickej energie sa rovná strednej hodnote potenciálnej energie. Tento vzťah platí i pri šírení harmonických deformácií v pružnom prostredí a <w_k> = <w_p>. Potom stredná hodnota hustoty celkovej mechanickej energie sa rovná w = w_k + w_p.

 

        (6.2.6.3)

 

Stredná hodnota hustoty energie  t.j. stredná energia obsiahnutá v jednotke objemu bude úmerná hustote prostredia, štvorcu amplitúdy šíriaceho sa vlnenia a uhlovej frekvencie.

 

Pre charakterizovanie výkonu prenášaného vlnením je účelné zaviesť pojem intenzita vlnenia.  Intenzita vlnenia sa rovná energii prenášanej postupujúcim vlnením jednotkou plochy kolmej na smer šírenia vlnenia za jednotku času.

 

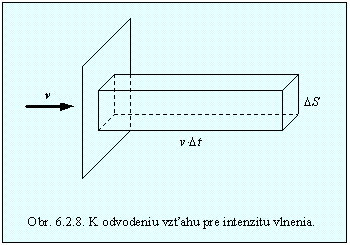
Nech vlnenie postupuje rýchlosťou t. Za čas Dt vlnenie postúpi o vzdialenosť vDt. Stredná energia prejdená plochou DS kolmou na smer šírenia vlnenia za jednotku času sa bude rovnať energii obsiahnutej  v objeme  vDtDS  (obr.6.2.8). Túto ľahko určíme, keď poznáme objem a strednú hustotu energie.

 

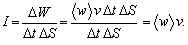        (6.2.6.4)

 

Jednotkou intenzity vlnenia je W m^-2.

 

 

Zatiaľ sme sa zaoberali iba vlnením v jednorozmernom prostredí (napr. strune), alebo rovinným vlnením šíriacim sa v trojrozmernom priestore, ktorého matematický poopis je rovnaký. Dôležitý je však aj prípad vlnenia, ktoré sa v homogénnom trojrozmernom prostredí šíri z bodového zdroja. Takéto vlnenie sa nazýva guľové, lebo jeho vlnoplochy sú guľové plochy. Pri šírení guľového vlnenia v homogénnom prostredí, v ktorom nedochádza k pohlcovaniu energie, celkový tok energie guľovou plochou ľubovoľného polomeru musí byť rovnaký.  Guľová plocha je úmerná r², preto intenzita vlnenia musí byť úmerná r^–2. Vzhľadom na to, že intenzita vlnenia je úmerná hustote energie a táto zas štvorcu amplitúdy, z predchádzajúceho vyplýva, že amplitúda  guľovej vlny musí klesať so vzdialenosťou a to úmerne r^–1.