Monochromatická harmonická vlna opísaná vlnovou funkciou (6.3.5) nie je v priestore ohraničená, nemá začiatok ani koniec a teda nekorešponduje s reálnym tvarom vlny. Je fyzikálnou abstrakciou. Princíp superpozície dovoľuje ľubovoľnú vlnu, aj nie harmonickú, vyjadriť superpozíciou harmonických vĺn diskrétneho, alebo spojitého spektra frekvencii. Takto vytvorená grupa vĺn, pre ktorú sa zaužíval názov „vlnový balík“, môže už predstavovať v priestore sa šíriacu reálnu vlnu. Rýchlosť postupu takéhoto vlnového balíka – grupová rýchlosť, sa rovná šíreniu energie (signálu) reálnou vlnou.

 

Najjednoduchší vlnový balík (jednoduchý, ale aj nedokonalý), ktorý nám umožní zaviesť a objasniť pojem grupová rýchlosť, vytvoríme zložením dvoch harmonických vĺn blízkych frekvencií a uhlových vlnových čísel.

Nech  w₁ = w + dw, k₁ = k + dk, w₂ = w – dw a k₂ = k – dk.  Príslušným vlnám odpovedajú vlnové funkcie

 

        (6.2.7.1)

 

        (6.2.7.2)

 

S využitím známeho trigonometrického vzorca pre súčet dvoch funkcií kosínus (Pr.6.2.6) možno výsledné vlnenie podľa princípu superpozície vyjadriť funkciou

 

        (6.2.7.3)

 

Táto funkcia predstavuje postupujúcu vlnu u(x,t) = u^’cos(wt –kx) s modulovanou amplitúdou.

 

        (6.2.7.4)

 

Pre zvolený bod x ide vlastne o skladanie kmitov s blízkymi frekvenciami w₁, w₂. Tento problém sme už vyriešili v časti 6.1.7.2, výsledný časový priebeh kmitania je graficky znázornený na obr.6.1.13. V dôsledku symetrického postavenia súradnice x a času t vo funkcii (6.2.7.3) má graf priestorovej závislosti vlny (výchylky), ktorú teraz skúmame, pre zvolený časový okamžik t rovnaký charakter, stačí v ňom čas t nahradiť súradnicou x a výchylku, ktorá bola v tomto grafe označená x označiť u. Amplitúda tejto vlny u₀’ je funkcia času a polohy. Vzhľadom na druhý súčiniteľ cos(wt –kx) vo vzťahu (6.2.7.3) sa mení pomerne iba pomaly, lebo dw  a dk sú vzhľadom na w a k malé. Za rýchlosť šírenia sa takejto vlny považujeme rýchlosť, ktorou sa šíri miesto v ktorom má amplitúda určitú konštantnú hodnotu.

Napríklad maximálnu amplitúdu majú miesta pre ktoré

 

tdw – x dk = 0        (6.2.7.5)

 

Rýchlosť šírenia sa takéhoto maxima vlnového balíka je grupová rýchlosť.

 

        (6.2.7.6)

 

Fázová rýchlosť je určená vzťahom (6.2.2.6) v_f = w /k. Vyjadrime z tohoto vzťahu w = kv_f a dosaďme do (6.2.7.6). Dostávame

 

        (6.2.7.7)

 

kde sme využili

 

 

Ak fázová rýchlosť závisí od uhlového vlnového čísla, teda ak je fázová rýchlosť rôzna pre rôzne vlnové dĺžky, potom dv_f/dl ¹0 a fázová rýchlosť sa nerovná grupovej rýchlosti. V našej vlne s modulovanou amplitúdou (6.2.7.3) by sa rozdiel medzi fázovou a grupovou rýchlosťou prejavil tak, že nosná vlna na obr. 6.1.13 (modifikovanom vo vyššie uvedenom zmysle) by postupovala inou rýchlosťou než jej obálka. Jav, kedy grupová rýchlosť je rôzna od fázovej rýchlosti voláme disperzia vlnenia. V optike sa disperzia svetla prejaví závislosťou indexu lomu od vlnovej dĺžky. Každý čitateľ si už istotne všimol rozklad bieleho svetla na vlnové dĺžky rôznej farby pri prechode svetla brúseným sklom, alebo skleneným hranolom.

 

 

Pre vlny s veľkou vlnovou dĺžkou, ktoré vznikajú na povrchu vody silou tiaže, je disperzia daná vzťahom

 

 

kde  v  je fázová rýchlosť vlnenia,  l  je vlnová dĺžka a  g  je tiažové zrýchlenie. Určte grupovú rýchlosť tohoto vlnenia.

 

Pre grupovú rýchlosť platí vzťah 

 

 

Aby sme podľa neho mohli určiť v_g,  potrebujeme vyjadriť deriváciu fázovej rýchlosti  v  podľa veľkosti uhlového vlnového vektora k.  Najvýhodnejšie sa dá táto derivácia urobiť, ak vyjadríme  v  ako funkciu  k  namiesto  l .  Keďže  l = 2p/k,  je fázová rýchlosť 

 

 

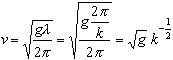
a  jej derivácia podľa veľkosti uhlového vlnového  vektora je

 

 

Potom  dostávame