Častice ideálneho plynu nepôsobia na seba navzájom vnútornými silami, a preto častice plynu nemajú potenciálnu energiu. Energia plynu, ktorá sa skladá z kinetických energií jeho častíc pohybujúcich sa chaotickým tepelným pohybom sa nazýva vnútorná energia plynu.

 

Ak budeme zohrievať nádobu s plynom, pričom steny nádoby sú pevné, dodávané teplo DQ sa zmení na nárast vnútornej, t.j. kinetickej energie plynu. Prírastok vnútornej energie plynu v nádobe je úmerný prírastku teploty plynu, množstvu častíc v nádobe a ich hmotnosti. Teplota plynu tu vystupuje ako nová veličina, ktorá je nejakým spôsobom zviazaná s pohybom častíc, resp. s ich kinetickou energiou. Môžeme napísať

 

        (a)

 

kde m je hmotnosť jednej častice plynu, c je konštanta charakterizujúca časticu plynu, N je počet častíc v nádobe. T₀ a U₀ sú teplota a vnútorná energia plynu pred ohrevom, T a U po ohreve (poznámka: veličina c v rovnici (a) vystupuje ako konštanta úmernosti vo vzťahu pre teplo prijaté plynom bez konania práce. Ak je častíc veľmi veľa, táto konštanta sa stáva hmotnostnou tepelnou kapacitou plynu pri konštantnom objeme). Z rovnice (a) vyplýva, že

 

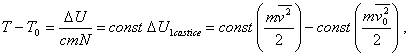        (b)

 

kde sme kinetickú energiu častice predstavili pomocou strednej kvadratickej rýchlosti, čím sme dostali strednú kinetickú energiu častice. Pri danej teplote môžeme si predstaviť súbor častíc ako súbor, v ktorom  každá častica má strednú kvadratickú rýchlosť, a teda aj strednú kinetickú energiu (táto predstava môže slúžiť len na vysvetlenie celkovej vnútornej energie plynu ako súčtu stredných kinetických energií častíc. V skutočnosti častice plynu majú rôzne rýchlosti). Stredná kvadratická rýchlosť charakterizuje celý súbor častíc.

 

Ako vidíme podľa (b), stredná kinetická energia častice priamo súvisí s teplotou plynu, ktorá je makroskopickou merateľnou veličinou. Tiež môžeme prehlásiť, že ak dva plyny majú rovnakú teplotu, potom stredné kinetické energie ich častíc (atómov, molekúl) sú rovnaké, a to aj vtedy, ak nádoby s plynmi sú od seba ľubovoľne vzdialené. Ak by sa plyn v nádobe skladal z dvoch druhov častíc s rôznymi hmotnosťami, tak všetky častice by mali tú istú strednú kinetickú energiu. To znamená, že ťažšie častice sa pohybujú pomalšie.

 

Vzťah (b) platí všeobecne. Skutočnosť, že jednej teplote zodpovedá jedna stredná kinetická energia častice nezávisle od druhu plynu, ukazuje, že konštanta úmernosti v rovnici (b) má rovnakú hodnotu pre každý plyn, t.j. je to univerzálna konštanta. Zvolíme ju ako

 

        (c)

 

Potom z (b) vyplýva pre strednú kinetickú energiu jednej častice

 

         (7.1.4)

 

Toto je základná rovnica kinetickej teórie plynu pre energie (tiež sa nazýva Boltzmannovou rovnicou) a tvrdí, že stredná kinetická energia posuvného pohybu častíc pri ich tepelnom pohybe je priamo úmerná teplote plynu (v kinetickej teórii plynov používame Kelvinovu teplotnú stupnicu).  Konštanta k = 1,381.10^-23 J.K^-1 je Boltzmannova konštanta, je to jedna zo základných fyzikálnych konštánt.

 

Zo vzťahu (7.1.4) vzhľadom na nemožnosť dosiahnuť T = 0 (čo je obsahom tretej vety termodynamickej) vyplýva, že nikdy neustane tepelný pohyb častíc plynu. To si ľahko môžeme predstaviť, ak si vezmeme malý objem v plyne a chceme v ňom dosiahnuť T = 0. To by znamenalo, že častice v tomto objeme musia energiu len odovzdávať časticiam v okolí a nijakú energiu od nich neprijímať. Pri chaotickom pohybe všetkých častíc je nemožné zorganizovať takýto proces výmeny energie. A keby sa to aj podarilo, nie je takýto stav možné trvalo udržať, lebo nemôžeme častice vnútri objemu uchrániť od zrážok s časticami z okolia a tým od zvýšenia ich kinetickej energie, čo má za následok zvýšenie teploty v sledovanom objeme.

 

Ak si vezmeme časticu plynu guľového tvaru zanedbateľných rozmerov, môžeme ju považovať za hmotný bod. Tento má 3 stupne voľnosti (t.j. jeho polohu v priestore udávajú tri voliteľné súradnice). Zo vzťahu (7.1.4) vyplýva, že na každý stupeň voľnosti pripadá energia kT/2. Toto rovnomerné rozdelenie energie medzi stupne voľnosti sa nazýva ekvipartičný teorém. Napriek tomu, že bol stanovený pre najjednoduchšiu časticu, zovšeobecňuje sa aj pre častice zložené, ktoré majú viac stupňov voľnosti.

 

Počet stupňov voľnosti pre dvojatómovú molekulu (napr. O₂) určíme takto: polohu jedného atómu určíme tromi voliteľnými súradnicami. Druhý atóm sa môže otáčať okolo prvého po guľovej ploche, ktorá má polomer rovnajúci sa dĺžke spojky oboch atómov. Polohu atómu na guľovej ploche určujú dve súradnice, t.j. spolu máme 5 voliteľných súradníc). Pre molekuly z viac ako 3 atómov počet stupňov voľnosti určíme ako v prípade dvojatómovej molekuly, ale pridáme ešte možný otáčavý pohyb tretieho atómu okolo osi tvorenej spojnicou prvých dvoch atómov. Polohu otočenej molekuly udáva jedna uhlová súradnica, t.j. spolu máme 6 voliteľných súradníc, alebo 6 stupňov voľnosti. Potom

 

        (7.1.5)

 

Pre i > 3 predpokladáme, že molekula predstavuje teleso, ktoré okrem posuvného pohybu môže vykonávať aj rotačný pohyb. Potom celková stredná energia molekuly má aj zložky prislúchajúce rotačnému pohybu. V zložitejšom prípade, keď molekula nie je tuhá a môžu v nej atómy kmitať, sa objavujú ďalšie zložky energie.

 

 

Klasická teória považuje voľné elektróny v kove za elektrónový plyn. Vypočítajte strednú kvadratickú rýchlosť elektrónu v kove, ak je teplota kovu 20 °C.

 

Použijeme (7.1.4), z ktorého vyplýva

 

 

Po dosadení T = 293 K a hmotnosti elektrónu m =9,11 .10^-31 kg a k = 1,381.10^-23    J/K  dostaneme  v_k = 1,162 . 10⁵ ms^-1

 

 

V nádobe s objemom 1 m³ je 1 kg argónu pri teplote 200 °C. Aká je stredná kvadratická rýchlosť? Koľko atómov argónu je v nádobe?

 

Zo vzorca (7.1.4) vypočítame strednú kvadratickú rýchlosť tak ako v príklade 7.1.3.1. Z periodickej tabuľky prvkov zistíme, že relatívna atómová hmotnosť argónu je 40, čo vynásobíme hmotnosťou nukleónu 1,67.10^-27 kg, čím získame hmotnosť atómu argónu (jednoatómový plyn): 6,68.10^-26 kg . Pri teplote T = 473 K je v_k = 541,6  m/s. Počet atómov v nádobe získame vydelením celkovej hmotnosti plynu hmotnosťou jedného atómu: