Doteraz sme sa zaoberali ideálnym plynom. Stavová rovnica ideálneho plynu sa hodí aj pre reálne plyny ak sú dostatočne zriedené. Ak nie, potom sa prejavuje objem častíc (ktorý nie je nulový) a sily vzájomného pôsobenia medzi časticami. Odvodenie s uvažovaním týchto činiteľov vedie k stavovej rovnici

 

        (7.1.30)

 

čo je van der Waalsova stavová rovnica pre 1 mól plynu. Ak máme m mólov, potom treba násobiť touto hodnotou veličiny, ktoré obsahujú počet častíc a rovnica nadobudne tvar

 

        (7.1.30a)

 

 Veličiny a, b sa pre daný plyn určia experimentálne, pričom výpočet ukazuje, že b je 4-násobok súhrnného objemu častíc.

 

Rovnica (7.1.30) je pre objem V rovnicou 3. stupňa a môže mať 1 alebo 3 reálne korene. Vzhľad van der Waalsových izoteriem je na obr. 7.1.9. Pre vysoké teploty sa krivky podobajú na Boyle-Mariottove izotermy. Tieto sú oddelené kritickou izotermou (s bodom K) od izoteriem, ktoré dávajú teoretickú možnosť troch objemov pre jeden tlak. V praxi však takéto izotermy nedokážeme získať. Ak napr. na obr. 7.1.10 postupujeme po izoterme dole (zvyšujeme objem a znižujeme tlak, čo je prirodzený proces), prídeme do bodu A. Ďalší postup po izoterme by znamenal súčasné rozpínanie plynu pri zvyšovaní tlaku, čo nie je

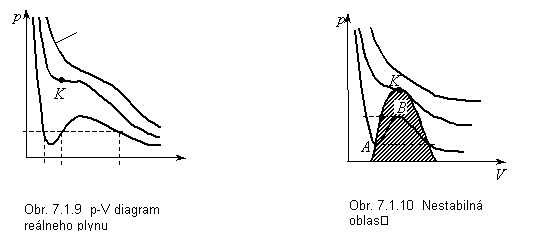
možné. Plyn prejde do stavu A₁ izobarickým procesom. Podobne, ak by sme postupovali po izoterme od veľkých objemov, prišli by sme do bodu B a ďalší postup by bol nemožný, lebo nedá sa naraz znižovať tlak aj objem. Plyn prejde do stavu B₁. Čiarkovaná plocha je oblasť nestabilného stavu. Napravo od nej (malé tlaky, veľké objemy) sú stavy, keď látka je plynná. Naľavo od nej (malé objemy, vysoké tlaky) je oblasť skvapalneného plynu. Zmena skupenstva prebieha práve v nestabilnej oblasti. Veľká strmosť izoteriem odráža fakt, že na malé zmenšenie objemu kvapaliny treba veľké zvýšenie tlaku. Ak je teplota plynu rovnaká alebo vyššia ako kritická, plyn sa nedá skvapalniť. V bode K sa stráca rozdiel medzi plynom a kvapalinou.