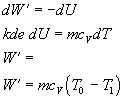Práca plynu pri izotermických procesoch
Práca plynu pri izotermických procesoch
V technickej praxi sa často stretávame so situáciou, kedy plyn uzavretý v nádobe s pohyblivou stenou ( piestom ) tento piest posunie v dôsledku svojej expanzie alebo kompresie. ( Pozri obr. 7.2.1.1 a paragraf 7.2.1.) Ak plyn posunul piest, hovoríme, že vykonal prácu. Pri jednotlivých termodynamických procesoch má práca svoje špecifické vyjadrenie.
a) Izobarická expanzia : p = konštanta.
Prácu vykonanú plynom vypočítame
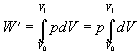 ( 7.2.4.1 )
( 7.2.4.1 )Po vykonaní predpísanej integrácie
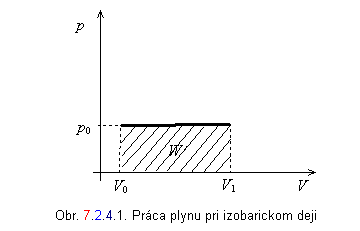
Plynom vykonaná práca sa rovná súčinu konštantného tlaku a rozdielu konečného a počiatočného objemu plynu. Práca je úmerná vyšrafovanej ploche obdĺžnika na obrázku 7.2.4.1.
b) Izotermická expanzia : T0 = konštanta.
S výpočtom práce pri izotermickom deji sme sa už stretli v paragrafe 7.2.3. Tieto poznatky môžeme rozšíriť nasledujúcim spôsobom.
Pri sledovaní plynom vykonanej práce budeme vychádzať zo vzťahu 7.2.4.1, kde tlak vyjadríme zo stavovej rovnice v tvare
a vo vzťahu vyjmeme pred integrál veličiny nemeniace sa v procese integrovania
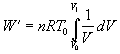
Po integrácii vzťahu v predpísaných medziach
Pri konštantnej teplote sústavy sa vnútorná energia nemení. Teplo dodané sústave sa prejaví len vo forme práce, ktorú sústava vykonala.
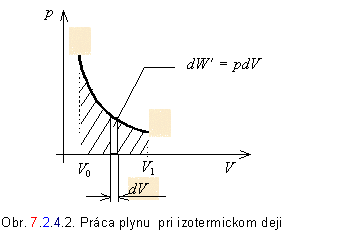
Veľkosť sústavou vykonanej práce za daných podmienok je úmerná vyšrafovanej ploche na obrázku č. 7.2.4.2 .
c) Adiabatická expanzia : dW¢ = -dU
Ak počítame prácu vykonanú plynom pri adiabatickom deji, jej veľkosť je daná vzťahom
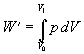
Z Poissonovho vzťahu vyjadríme tlak
a dosadíme do poslednej rovnice
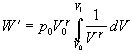
Po zintegrovaní v predpísaných hraniciach
Keďže Poissonovu rovnicu môžeme napísať aj v tvare
posledný vzťah nadobudne tvar
Prácu vykonanú pri adiabatickej expanzii plynu môžeme vypočítať pomocou konečných a počiatočných hodnôt stavu objemu a tlaku plynu. Uplatnením stavovej rovnice v tvaroch p0V0 = nRT0 a p1V1 = nRT1 môžeme vzťah napísať v tvare
Upravme teraz Mayerov vzťah
R = CP - CV = McP - McV = M(cP - cV) = M(gcV - cV) = - McV(1 -g )
a dosaďme do rovnice 7.2.4.4 . Ak vyjadríme aj látkové množstvo n = m/M a rovnicu upravíme, dostávame vzťah
Vzťah nám hovorí, že prácu vykonanú plynom pri adiabatickej expanzii môžeme vypočítať aj pomocou rozdielu počiatočnej a konečnej hodnoty teploty a práca je konaná na úkor vnútornej energie plynu. V praxi za adiabatické deje považujeme aj deje prebiehajúce veľmi rýchlo. Tak rýchlo, že nestihla prebehnúť výmena tepla s okolím.
Príklad 7.2.4.1
Aká veľká práca je potrebná na stlačenie kyslíka uzavretého v nádobe s pohyblivým piestom objemu V0 = 0,5m3 a tlaku p0 = 105 Pa na tlak p1 = 3,5.105 Pa, ak stláčanie vykonáme a) izotermicky, b) adiabaticky ?
Riešenie
a) Pri izotermickom deji je vnútorná energia konštantná a pre riešenie príkladu vyhovuje rovnica 7.2.4.2, v ktorej využijeme stavovú rovnicu nRT0 = p0 V0 a dostávame
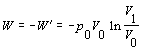
V rovnici sme vyjadrili vzťah medzi prácou vykonanou plynom a prácou vykonanou vonkajšími silami zmenou znamienka. Využitím stavovej rovnice pre konštantné veličiny n, R, T, nahradíme vo vzťahu
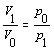
Potom
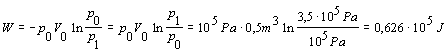
Na izotermické stlačenie kyslíka v nádobe je potrebná vonkajšia práca 0,626 . 105 J.
b) Pri adiabatickom deji sa neuskutočňuje výmena tepla s okolím . Pri výpočte využijeme rovnicu 7.2.4.3 v tvare
Ďalej rovnicu matematicky upravíme
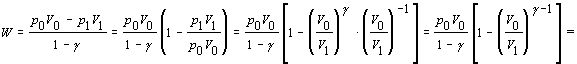
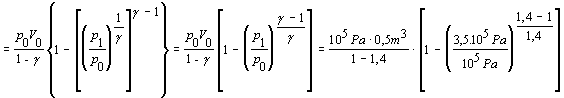
Pri úpravách sme využili rovnosti vyplývajúce z Poissonovej rovnice 7.2.3.5 v nasledujúcich tvaroch
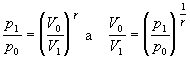
Číselnú hodnotu Poissonovej konštanty sme vypočítali zo známeho počtu stupňov voľnosti pre molekulárny kyslík i = 5 využitím vzťahu 7.1.14 .
Na adiabatické stlačenie kyslíka je potrebná práca 0,538 . 105 J.
Príklad 7.2.4.2
Neznámemu plynu s hmotnosťou m = 0,2 kg sme dodali teplo, v dôsledku ktorého sa jeho teplota zvýšila zo 60 0C na 95 0C a svojou expanziou vykonal prácu 1817J. O aký plyn ide ?
Riešenie
Zo zadania označíme t0 = 60 oC, t1 = 95 oC, 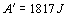 . Plyn sa budeme snažiť identifikovať pomocou hodnoty fyzikálnej veličiny, ktorá plyn charakterizuje a je možné vyjadriť ju pomocou zadaných veličín. V našom prípade sa jedná o molárnu hmotnosť. Východzím vzťahom bude vzťah pre výpočet práce vykonanej na plyne účinkom vonkajších síl
. Plyn sa budeme snažiť identifikovať pomocou hodnoty fyzikálnej veličiny, ktorá plyn charakterizuje a je možné vyjadriť ju pomocou zadaných veličín. V našom prípade sa jedná o molárnu hmotnosť. Východzím vzťahom bude vzťah pre výpočet práce vykonanej na plyne účinkom vonkajších síl
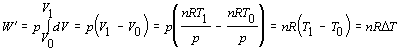
Matematickou úpravou vypočítame molárnu hmotnosť
Pomocou tabuliek zistíme, že v príklade sa jedná o plyn - kyslík.
Kontrolné otázky
-
Vysvetlite, ako môže plyn konať mechanickú prácu.
-
Povedzte praktický príklad, keď plyn koná prácu.
-
Ako by ste graficky porovnali veľkosť plynom vykonanej práce pri izotermickom a izobarickom deji?
-
Ktoré deje v praxi považujeme za adiabatické ak vieme, že sústavu od okolia dokonale tepelne izolovanú prakticky nie je možné vytvoriť?
-
Aký logický krok by ste doplnili do nasledujúcej postupnosti? (Porovnajte s 7.2.4.c.),
položme dQ = 0
-
Vo valci s pohyblivým piestom je pri teplote 273K a tlaku 101kPa uzavretých 5m3 vzduchu.O koľko musíme zohriať tento plyn, ak má izobaricky vykonať prácu 100kJ? ( DT=54K )
-
Akú prácu vykonal kyslík s hmotnosťou 0,1kg, začiatočnou teplotou 20°C a tlakom 2MPa, ktorý počas rozpínania klesol na hodnotu 1,8MPa.? Dej prebiehal a) izochoricky,b) izotermicky,c) adiabaticky.( a) W´=0J, b) W´=802J, c) W´=580J )