Rozpínajúci sa plyn môže vykonávať mechanickú prácu na úkor svojej vnútornej energie alebo na úkor tepla odoberaného z okolitých telies ( z ohrievača ). Také zariadenie, ktoré je schopné meniť tepelnú energiu na mechanickú prácu je napríklad parný stroj. Samotný pohybujúci sa piest vo valci však ešte nemôžeme považovať za tepelný stroj, lebo po určitej dobe piest dosiahne okraj valca a zastaví sa. Pod pojmom stroj rozumieme také zariadenie, ktoré je schopné vykonávať prácu neobmedzene dlho. Je teda potrebné piest vrátiť späť, pričom plyn odovzdá určité teplo okolitým telesám s nižšou teplotou ( chladiču ) a dej zopakovať. Piest stroja musí vykonávať periodický pohyb. Plyn dá do pohybu piest, ktorý sa po takomto periodickom deji vráti opäť do východiskového stavu - vykoná kruhový dej.

 

 

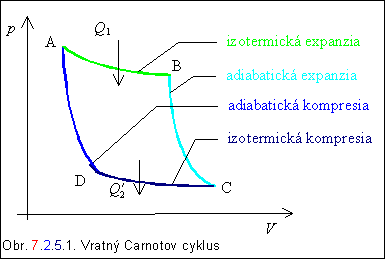
Kruhový dej v plyne môžeme uskutočniť viacerými postupmi. Najvyššiu účinnosť však dosiahneme realizáciou tzv. vratného Carnotovho cyklu (obr. 7.2.5.1 ).

 

Celý Carnotov cyklus je zložený z dvoch izotermických a dvoch adiabatických dejov, počas ktorých prácu vykonanú plynom opisujú nasledujúce rovnice:

–      izotermický dej medzi bodmi AB:

        plyn sa rozpína z objemu V_A na V_B, pričom prácu koná na úkor tepla dodaného zvonku pri konštantnej teplote T₁

 

        ( 7.2.5.1 )

 

–      adiabatický dej medzi bodmi BC:

        rozpínanie plynu pokračuje, ale práca sa koná na úkor vnútornej energie ( teplota plynu klesne z T₁ na T₂ ), lebo teplo dodané zvonka je nulové

 

        ( 7.2.5.2 )

 

–      izotermický dej medzi bodmi CD:

        pri kompresii plynu z objemu V_C na V_D sa pri konštantnej teplote T₂ uvoľní z plynu teplo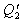

 

        ( 7.2.5.3 )

 

–      adiabatický dej medzi bodmi DA:

        kompresia plynu pokračuje, teplo však nie je odvádzané chladiču, ale sa prejaví zvýšením vnútornej energie plynu, jeho teplota vzrastie z T₂ na T₁

 

        ( 7.2.5.4)

 

V obrázku a vo vzťahoch 7.2.5.1 až 7.2.5.4 veličina T₁ označuje teplotu ohrievača a T₂ teplotu chladiča parného stroja.

 

Celková práca vykonaná počas jedného cyklu je úmerná ploche ohraničenej krivkou ABCD a je daná vzťahom

 

        ( 7.2.5.5)

 

Po dosadení rovníc 7.2.5.1 až 7.2.5.4 a zohľadnení skutočnosti, že  nC_V(T₁ - T₂) = - nC_V(T₂ - T₁) vidíme, že súčtom prvého a tretieho člena dostaneme nulu a vzťah 7.2.5.5 dostáva tvar

 

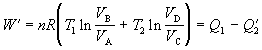        ( 7.2.5.6)

 

Na prácu pri Carnotovom cykle sa premení tá časť energie, ktorá je rozdielom medzi teplom plynu dodaným Q₁ a z plynu odvedeným .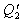

 

Ako sme už spomenuli, účinnosť Carnotovho cyklu je najvyššia. Vypočítame ju ako podiel energie premenenej na prácu a energie stroju dodanej, teda

 

 

Do rovnice dosadíme vzťahy 7.2.5.1 a 7.2.5.6 a jej pravú stranu rozdelíme na dva zlomky so spoločným menovateľom

 

 

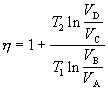
Ak vymeníme v čitateli v argumente logaritmu čitateľa s menovateľom, dostávame

 

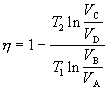        ( 7.2.5.7 )

 

Zapíšme si teraz stavovú rovnicu pre obidva izotermické a Poissonovu rovnicu pre obidva adiabatické deje

 

        ( 7.2.5.8 )

 

        ( 7.2.5.9 )

 

        ( 7.2.5.10 )

 

        ( 7.2.5.11 )

 

Upravme túto sústavu rovníc nasledujúcim postupom. Najskôr upravme rovnicu 7.2.5.10 , do ktorej dosadíme vzťahy 7.2.5.9 a 7.2.5.11 .

 

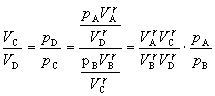        ( 7.2.5.12 )

 

Rovnicu 7.2.5.8 upravíme do tvaru 

 

 

dosadíme do 7.2.5.12 a dostávame

 

 

Obe strany rovnice vynásobíme výrazom 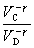 a čitateľa 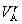s menovateľom 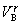na pravej strane vzájomne vymeníme s opačným znamienkom exponenta. Potom

 

 

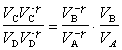
Upravíme čitateľov oboch strán rovnice

 

        ( 7.2.5.13 )

 

Z rovnosti vo vzťahu 7.2.5.13 vyplýva, že rovnicu 7.2.5.7 môžeme zjednodušiť na tvar

 

        ( 7.2.5.14 )

 

Vidíme, že účinnosť Carnotovho cyklu závisí len od teploty ohrievača a chladiča.

Uplatnenie Carnotovho cyklu rozširuje Carnotova veta:

 

 

 

Aká je teplota chladiča ideálneho parného stroja pracujúceho podľa reverzibilného Carnotovho cyklu, ak jeho účinnosť je 33% a teplota ohrievača je 190 ⁰C?

 

Účinnosť stroja opísaného v príklade vypočítame podľa vzťahu 7.2.5.14 . Jeho matematickou úpravou získame vzťah pre výpočet teploty chladiča T₂ .

 

 

V príklade sme označili účinnosť stroja  h=33%=0,33,   teplotu ohrievača   t₁=190⁰CÞT₁ =463,15K.

Teplota chladiča ideálneho parného stroja je 37,16 ⁰C.