Definujme celkovú hybnosť sústavy častíc ako vektorový súčet hybností jednotlivých častíc

 

        (1)

 

kde m_i je hmotnosť i-tej častice a v_i  je rýchlosť i-tej častice. Celkovú hybnosť sústavy hmotných bodov môžeme vyjadriť i cez myslený hmotný bod, ktorý sa nachádza v hmotnom strede sústavy a v ktorom je sústredená celková hmotnosť.  Rýchlosť hmotného stredu získame deriváciou jeho polohového vektora určeného  vzťahom (3.1.1.3):

 

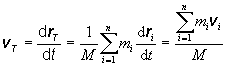        (2)

 

Pre jeho hybnosť  platí

 

        (3)

 

Celková hybnosť sústavy hmotných bodov sa rovná hybnosti mysleného bodu, ktorý sa nachádza v hmotnom strede sústavy. Tento bod sa pohybuje rovnakou rýchlosťou  s akou sa pohybuje hmotný stred a má hmotnosť celkovej hmotnosti sústavy.  Zrýchlenie  hmotného stredu dostaneme deriváciou vzťahu (3):

                                                                                                          

 

        (4)

 

Ľavú stranu rovnice (4) možno vyjadriť pomocou síl pôsobiacich v sústave:

 

        (5)

 

V poslednom súčte každý člen znamená celkovú silu pôsobiacu na i-ty hmotný bod. Uvažujme teraz sily pôsobiace na každý hmotný bod sústavy. Nakoľko pre i-tu časticu platí Newtonov zákon, možno pohybovú rovnicu pre sústavu hmotných častíc, na základe  vzťahu   (3.1.2.5)   vyjadriť

 

        (6)

 

resp. pomocou celkovej hybnosti sústavy hmotných bodov ako

 

        (7)

 

V sústave hmotných bodov sme pre hybnosť i-teho hmotného  bodu použili označenie H_i  oproti označeniu p_i používanom  pri hmotnom bode. Obidve označenia sú synonymá a bežne sa v rôznych učebniciach používajú.