 Odvodenie Keplerových zákonov
Odvodenie Keplerových zákonov
Odvodenie Keplerových zákonov z Newtonovho gravitačného zákona
Kvôli jednoduchosti predpokladajme nie eliptické, ale kruhové dráhy dvoch planét s polomermi r1 a r2. Vychádzame z Newtonovho zákona sily, ktorý pre prvú planétu s hmotnosťou m1 má tvar
F1 = m1a1 (3.2.2.5)
a1 je dostredivé zrýchlenie planéty. Toto, ako vieme z kinematiky, môžeme vyjadriť pomocou uhlovej rýchlosti alebo periódy obehu ako
Jeho dosadením do vzťahu (3.2.2.5 ) dostaneme
Sila F1 je zároveň totožná s gravitačnou silou, ktorú vyjadruje Newtonov gravitačný zákon
ms je hmotnosť Slnka. Porovnaním vzťahov (3.2.2.7 ) a (3.2.2.8 ) dostaneme
Keď urobíme rovnaký výpočet pre druhú planétu, dostaneme analogický výsledok
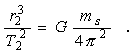 (3.2.2.10)
(3.2.2.10)Porovnaním ľavých strán oboch posledných vzťahov dostaneme
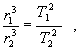
čo je vyjadrením 3. Keplerovho zákona, ktorý sme chceli dokázať.

