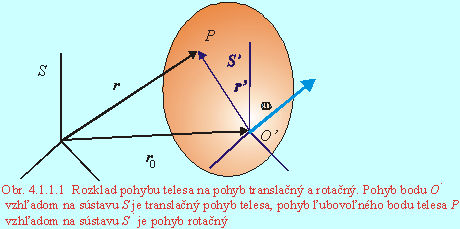
Vyjadrime všeobecný pohyb telesa ako súčasný translačný a rotačný pohyb. Pohyb telesa sledujme vo vzťažnej sústave S. Zvoľme si pomocnú sústavu S ´, ktorej začiatok je pevne viazaný na určitý bod telesa napr. O´ a jej osi sú rovnobežné s osami sústavy S (Obr.4.1.1.1). Potom pohyb súradnicovej sústavy S ´, pevne spojenej s telesom v bode O ´, opisuje translačný pohyb telesa. Bod P vzhľadom na bod O ´ má pevnú vzdialenosť, jej veľkosť vzhľadom na sústavu S ´ sa nemení. Relatívne vzhľadom na S´ sa bod P môže pohybovať len rotačným pohybom uhlovou rýchlosťou w. Z kinematiky zloženého pohybu hmotného bodu vyplýva, že rýchlosť bodu P vzhľadom na sústavu S je daná vzťahom:

 

 

 

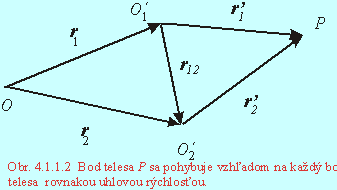
Pohyb sa skladá z translačného pohybu daného rýchlosťou v₀ bodu O ´ a rotačného pohybu telesa vzhľadom na S´ daného uhlovou rýchlosťou w. Pritom táto uhlová rýchlosť nezávisí od voľby bodu O ´. O tom sa môžeme presvedčiť voľbou ďalšej vzťažnej sústavy. Zvoľme si dve nové vzťažné sústavy s začiatkami  O₁^´ a O₂^´ (Obr. 4.1.1.2). Pre rýchlosť bodu P vyjadrenú pomocou týchto vzťažných sústav platí

 

 

Keď vyjadríme rýchlosť bodu O₂^´ pomocou bodu O₂^´:

 

 

a dosadíme takto vyjadrenú rýchlosť v₂ do prvej rovnice, dostávame rovnosť oboch uhlových rýchlostí:

 

           

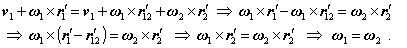
Príkladom môže byť valenie gule po naklonenej rovine: Pohyb rozložíme na translačný pohyb (hmotného) stredu gule a rotáciu okolo tohto stredu. Pohyb môžeme vyjadriť aj ako rotáciu telesa okolo dotykovej priamky. Presunutím pomocného bodu do bodu dotyku gule s podložkou, uhlová rýchlosť otáčania sa nezmení.