Odvodenie vzorca pre strednú voľnú dráhu
Odvodenie vzorca pre strednú voľnú dráhu
Sledujme jednu časticu, ktorá sa pohybuje strednou rýchlosťou a zatiaľ predpokladajme, že sa pohybuje bez ohľadu na zrážky priamočiaro a že za dobu Dt narazí na iné častice, ktorých stredy sú vo valci s priemerom 2d, kde d je priemer častice (t.j. tieto častice zasahujú do valca s priemerom d). Nami sledovaná častica sa pohybuje pozdĺž osi valca. Tiež budeme predpokladať, že ostatné častice sa nepohybujú. Ak je n koncentrácia častíc v nádobe, potom počet zrážok za dobu Dt bude
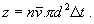(a)Teraz urobíme opravu na pohyb ostatných častíc. Namiesto strednej rýchlosti musíme
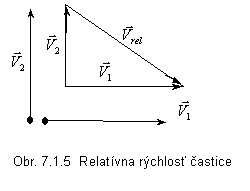
vziať strednú relatívnu rýchlosť sledovanej častice voči inej častici. Vektory rýchlostí dvoch častíc v1, v2 môžu zvierať uhol 0 - 180°. Keďže všetky smery sú rovnako pravdepodobné, stredný uhol medzi vektormi rýchlostí je (180+0)/2 = 90°. Ak sa častice 1, 2 pohybujú strednou rýchlosťou a ich dráhy zvierajú uhol 90°, bude podľa obr. 4.1.5 vrel = v1 – v2 .
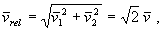
čo dosadíme do vzťahu (a) miesto strednej rýchlosti:
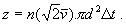(7.1.15)Stredná voľná dráha sa bude rovnať dráhe sledovanej častice prejdenej za dobu Dt delenej počtom zrážok. Takto dostaneme dráhu medzi dvomi zrážkami
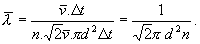(7.1.16)