Nakoľko podstata prenosu rôznych veličín je rovnaká, vyriešime prenos cez plôšku dS najprv všeobecne. Označíme si prenášanú veličinu ako B a jej strednú hodnotu týkajúcu sa jednej častice plynu ako b. Plôška delí priľahlý priestor na oblasti 1 a 2. Na jednej strane plôšky dS nech je stredná hodnota sledovanej veličiny b₁ a na druhej strane b₂. Tieto veličiny musia byť rôzne, ináč by prenos zo strany 1 na stranu 2 bol rovnaký ako zo strany 2 na stranu 1. Ďalej označíme dN₁ počet častíc, ktoré prejdú zo strany 1 na stranu 2 a dN₂ počet častíc, ktoré prejdú zo strany 2 na stranu 1.

 

Cez plôšku dS sa prenesie zo strany 1 na stranu 2 množstvo veličiny

 

 

a v opačnom smere

 

 

Výsledný prenos je

 

        (a)

 

Určíme teraz množstvá častíc dN. V prvom rade musíme obmedziť trvanie prenosu, budeme ho sledovať počas intervalu dt. Vzhľadom na chaotickosť pohybu môžeme si predstaviť (tak ako sme to urobili pri odvodení vzťahu pre tlak plynu v § 4.1.1), že 1/3 častíc plynu sa pohybuje kolmo na plôšku dS a z nich 1/2 jedným smerom, t.j. v danom okamihu sa pohybuje smerom k plôške zo strany 1 na stranu 2 práve 1/6 častíc nachádzajúcich sa v priľahlom priestore okolo plôšky dS. Cez plôšku prejdú za čas dt len tie častice, ktoré nie sú od nej vzdialené viac ako 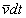, kde 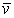 je stredná rýchlosť častice.  To znamená, že prejdú len tie častice, ktoré sú v objeme valca so základňou dS a výškou 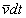, t.j. ktoré sú v objeme  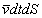a majú smer pohybu kolmý na plôšku. Z týchto úvah vyplýva, že

 

 

 

kde n₁ a n₂ sú koncentrácie častíc na rôznych stranách plôšky. Po dosadení do (a)

 

        (b)

 

Veličina D(bn) znamená zmenu množstva prenášanej veličiny, pričom bn predstavuje jej množstvo obsiahnuté v objeme 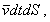t.j. jej koncentráciu. Znamienko mínus vyjadruje skutočnosť, že veličina B sa prenáša tam, kde je jej koncentrácia menšia, t.j. v smere zmenšovania jej koncentrácie, čo sa vyjadrí ako .

 

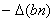Zistíme teraz čomu sa rovná D(bn). Nech plôška dS je kolmá na smer najväčšej zmeny bn. Tento smer nech je smer osi x. Potom derivácia

 

 

charakterizuje strmosť zmeny bn pozdĺž osi x. (Pozn: keďže smer x je smer najstrmšej zmeny bn, táto derivácia predstavuje gradient bn). Môžeme napísať (podľa matematických pravidiel)

 

        (c)

 

kde D(bn) je zmena bn na úseku Dx.  Odhadneme Dx. Cez plôšku dS budú preletovať častice s rôznou voľnou dráhou. Pre výpočet môžeme predpokladať, že k plôške sa z oboch strán dostanú častice, ktoré majú strednú voľnú dráhu,

 

 

Po dosadení do (c):

 

 

a ďalej do (b): 

 

 

Dostali sme takto všeobecný vzťah pre prenos nejakej veličiny B cez plôšku dS za čas dt a to v dôsledku tepelného pohybu častíc plynu, ktoré sa pohybujú strednou rýchlosťou 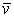a ktoré majú strednú voľnú dráhu

 

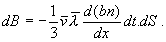        (d)