 Výpočet tlaku plynu na stenu nádoby
Výpočet tlaku plynu na stenu nádoby
Zvolíme si nádobu v tvare kocky s hranou L a zavedieme súradnicovú sústavu s osami x, y, z, ktoré budú rovnobežné s hranami kocky. Ako už vieme, častice plynu sa pohybujú chaoticky a nijaký smer vektora rýchlosti v nemá prednosť pred iným smerom, t.j. každý smer rýchlosti v je rovnako pravdepodobný. To nám umožňuje urobiť si predstavu, že 1/3 častíc sa pohybuje v smere osi x, 1/3 v smere osi y a 1/3 v smere osi z. Pre ďalšie odvodzovanie stačí uvažovať len jeden smer.
Častica, ktorá letí oproti stene má hybnosť mv. Smer jej pohybu je kolmý na stenu a po náraze bude mať častica hybnosť -mv, pretože náraz je pružný a častica pri ňom nestráca kinetickú energiu. Znamienko mínus vyjadruje, že častica sa po náraze pohybuje opačným smerom. Impulz sily pôsobiacej na stenu bude
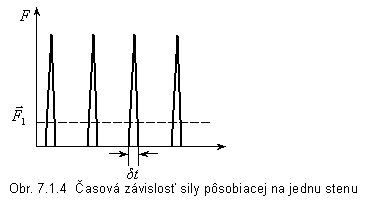
kde F0 je sila, ktorá vznikne nárazom na stenu, dt je trvanie nárazu. Ako vidíme, orientácia sily je rovnaká ako orientácia hybnosti pred nárazom, t.j. do steny. Častica letí k protiľahlej stene, odrazí sa od nej, letí zase späť atd. Časová závislosť sily vznikajúcej nárazmi častice na tej istej stene je na obr. 4.1.4. Za dobu Dt častica nalieta v nádobe vzdialenosť l = v. Dt . Vzdialenosť l je zložená z úsekov L. Počet preletov častice v nádobe za dobu Dt bude
a počet nárazov na jednu stenu vDt/2L. Celkový impulz sily na jednu stenu od jednej častice za dobu Dt je úmerný počtu impulzov
kde vystupuje stredná hodnota sily pôsobiacej od nárazov jednej častice na stenu. Za jednotku času bude na stenu pôsobiť impulz Dt krát menší. Iné častice môžu mať iné rýchlosti, potom aj stredná sila bude od nich iná. Výsledná sila od všetkých častíc dopadajúcich na jednu stenu (ktorých je N/3, kde N je počet častíc v nádobe) bude
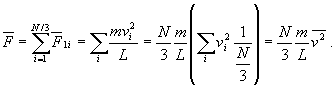
Výraz v zátvorke je stredná hodnota štvorca rýchlosti vi . Jej druhú odmocninu
nazývame strednou kvadratickou rýchlosťou. Tlak na stenu je
Veličina n je koncentrácia častíc.

