 Fraunhoferove a Fresnelove pribíženie
Fraunhoferove a Fresnelove pribíženie
V predchádzajúcom výpočte rozloženia intenzity svetla v okolí hranatého otvoru sme predpokladali, že svetelné lúče vychádzajúce z rozličných bodov otvoru sú navzájom paralelné. Toto priblíženie, ktoré sa nazýva Fraunhoferove priblíženie dáva dobré výsledky ak počítame intenzitu osvetlenia v dostatočnej vzdialenosti od otvoru, keď odchýlka od rovnobežnosti nespôsobuje podstatnú chybu. Z matematického hľadiska ide o náhradu pôvodne guľových vĺn rovinnými vlnami. V malých vzdialenostiach od otvoru sa chyba tohto priblíženie neprejaví v angulárnej (uhlovej) zložke rozloženia intenzity, ale hlavne v radiálnej zložke, ktorá je nepriamo úmerná kvadrátu vzdialenosti od otvoru:
![]() (12.9.1.)
(12.9.1.)
Na obrázku A je nakreslená angulárna zložka intenzity svetla v okolí kruhového otvoru vypočítaná použitím Fraunhoferovej teórie difrakcie.
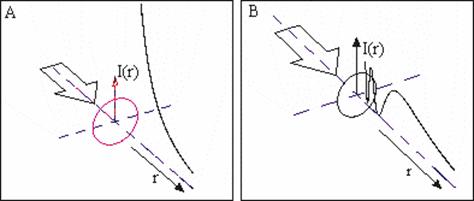
Vidíme, že intenzita v tesnej blízkosti otvoru diverguje do nekonečna, čo sa v experimente nepozoruje. Divergencia intenzity v tesnom okolí otvoru je priamym dôsledkom výmeny guľových vĺn za rovinné.
Presnejšiu aproximáciu (presné riešenie obvykle neexistuje) odvodil A. J. Fresnel (1788-1827) tak, že uvážil vplyv guľových vĺn v tesnom okolí otvoru. Podľa tohto priblíženia možno intenzitu svetla v ľubovoľnom bode P v okolí otvoru vyjadriť podľa vzťahu:
![]() (12.9.2.)
(12.9.2.)
kde: B2(R) je intenzita svetla v bode R umiestnenom v rovine otvoru (nie je konštantná) C a S sú Fresnelove integrály:
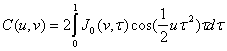 (12.9.3.)
(12.9.3.)
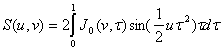 (12.9.4.)
(12.9.4.)
kde: J0 je Besselova funkcia, a je priemer otvoru, f je frekvencia dopadajúceho svetla
![]() (12.9.5.)
(12.9.5.)
Na obrázku B vidieť, že intenzita svetla v tesnej blízkosti otvoru osciluje, čo je hlavný rozdiel medzi Fraunhoferovou a Fresnelovou aproximáciou.
