 Výpočet elektrostatického poľa v niektorých špeciálnych prípadoch
Výpočet elektrostatického poľa v niektorých špeciálnych prípadoch
Elektrostatické pole na osi rovnomerne nabitej kruhovej dosky
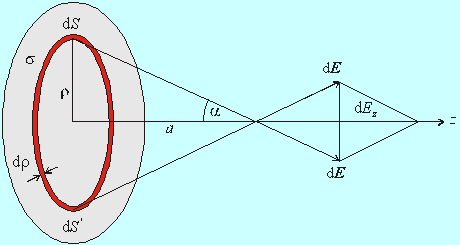
Na obr. 8.6.1.1 je znázornená kruhová doska, ktorá je rovnomerne pokrytá nábojom s plošnou hustotou s. (Môžeme si predstaviť, že náboj sa nachádza na každej strane dosky s polovičnou hustotou).
Vyberme si na doske malý plošný element dS vo vzdialenosti r od stredu dosky. Na obrázku je znázornený príspevok dE k celkovej intenzite E na osi vo vzdialenosti a od stredu. Z kruhovej symetrie dosky je zrejmé ( a preto počítame pole iba na osi dosky), že ku každému elementu dS existuje na protiľahlej strane dosky rovnako veľký element dS´, ktorého príspevok dE´ bude zrkadlovým obrazom príspevku dE vzhľadom na rovinu, ktorá prechádza osou dosky a je kolmá na obrázok. Z obrázku je zrejmé, že u každej takejto dvojice elementov sa zložky kolmé na os (z) dosky vyrušia a príspevky rovnobežné s osou dosky sa algebraicky sčítajú. To znamená, že ďalej nám stačí počítať iba príspevky k poľu iba v tomto jedinom smere.
![]() (8.1.6.1.1)
(8.1.6.1.1)
Všetky náboje, ktoré sa nachádzajú vo vzdialenosti r od stredu dosky dávajú rovnaký príspevok dEz. Preto môžeme plošný element dS voliť ako medzikružie s polomerom r a hrúbke dr. Plošný element dS = 2pr dr.
Potom
Obr. 8.1.6.1.1
Elektrostatické pole na osi rovnomerne nabitej dosky
![]() (8.1.6.1.2)
(8.1.6.1.2)
Výsledná intenzita má jedinú nenulovú zložku v smere osi z, čiže
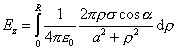 (8.1.6.1.3)
(8.1.6.1.3)
Keďže
![]()
tak
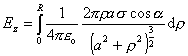 (8.1.6.1.4)
(8.1.6.1.4)
Zavedením substitúcie t = (a2 + r2) , ( dt = 2rdr) dostaneme
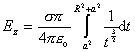 (8.1.6.1.5)
(8.1.6.1.5)
kde sme konštantné veličiny vyňali pred integrál. Integrovanie sa týka jednoduchej mocninnej funkcie, takže pre výsledné pole dostaneme
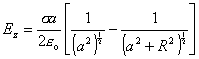 =
= 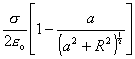 (8.1.6.1.6)
(8.1.6.1.6)
Výsledok ku ktorému sme dospeli má však iba obmedzenú platnosť pre os dosky. Zaujímavý je však limitný prípad, keď bod pozorovania je tesne nad stredom dosky a/R -> 0 a vtedy dostávame
![]() (8.1.6.1.7)
(8.1.6.1.7)
Tento výsledok môžeme interpretovať aj inakšie, a to tak, že budeme považovať vzdialenosť a za konečnú, ale polomer dosky R budeme neobmedzene zväčšovať. Tým sa dostávame k abstrakcii nekonečnej nabitej roviny, pre ktorú je každá priamka kolmá na rovinu jej osou. Pripomíname, že ide o idealizáciu, v praxi sa môžu vyskytovať nabité roviny iba konečných rozmerov.
Elektrostatické pole rovnomerne nabitého nekonečne dlhého vlákna
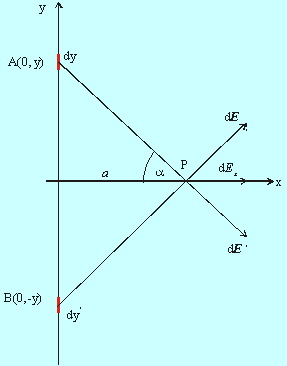
Obr.8.1.6.2.1
Predstavme si dlhé tenké vlákno, ktoré je elektricky nabité s konštantnou dĺžkovou hustotou l. Pozri obr.8.1.6.2.1 Zaveďme si súradnicovú sústavu x, y, z tak, že os y je spojená s vláknom a os x pre-chádza bodom pozorovania P, ktorý je vo vzdialenosti a od nabitého vlákna. Element vlákna v bode A(0, y) s dĺžkou dy generuje príspevok dE k výslednému elektrickému poľu E. Ku každému takémuto elementu však v bode B(0,-y) existuje element dy´, ktorý generuje príspevok dE´, taký, že y-ové zložky vektorov dE a dE´sa vyrušia. Preto nám ďalej stačí počítať iba x-ové zložky jednotlivých vektorov.
![]() (8.1.6.2.1)
(8.1.6.2.1)
Keďže
![]()
tak dostaneme
![]() (8.1.6.2.2)
(8.1.6.2.2)
V tomto prípade sa pokúsime vypočítať integrál trigonometrickou substitúciou
![]()
Pričom
![]()
Po dosadení dostávame
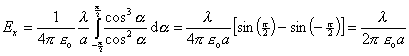
Teda
![]() (8.1.6.2.3)
(8.1.6.2.3)
Výsledok, ktorý sme dostali, je zaujímavý z toho hľadiska, že výsledný vektor poľa je kolmý na nabité vlákno a jeho veľkosť klesá s prvou mocninou vzdialenosti od vlákna. Samozrejme, nekonečne dlhé nabité vlákno je iba abstrakcia. V skutočnosti existujú iba nabité vlákna konečnej dĺžky. V takom prípade vzťah (8.1.6.2.3) platí iba v tesnej blízkosti vlákna. Vo vzdialenostiach oveľa väčších ako je dĺžka vlákna bude pole závisieť od celkového náboja na vlákne a klesať so štvorcom vzdialenosti.
Elektrostatické pole medzi dvoma nabitými rovinami
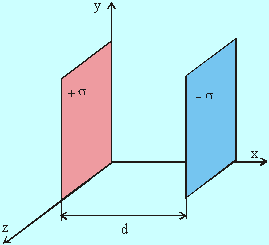
Obr. 8.1.6.3.1
Doskový kondenzátor
V praxi sa často stretávame s prípadom dvoch rovinných plôch s veľkosťou S, ktoré sú nabité rovnako veľkým nábojom opačného znamienka. Vzdialenosť medzi plochami d je obvykle veľmi malá v porovnaní s ![]() . Takéto zariadenie predstavuje doskový kondenzátor o čom však budeme pojednávať neskôr. Tu nám ide iba o výpočet elektrického poľa. V tomto prípade môžeme využiť výsledky získané v odseku 8.1.6.1 a uplatniť princíp superpozície. Situáciu znázorňuje obr. 8.1.6.3.1. Prvá plocha je daná rovinou x = 0 a je na nej rozložený náboj s plošnou hustotou s . Druhá plocha je daná rovinou x = d a je na nej náboj s plošnou hustotou - s. Zaujímame sa o elektrické pole v okolí týchto plôch a medzi nimi. Pre polia blízko nabitej plochy použiť aproximáciu (8.1.6.1.7) Musíme pritom rozlišovať 3 oblasti:
. Takéto zariadenie predstavuje doskový kondenzátor o čom však budeme pojednávať neskôr. Tu nám ide iba o výpočet elektrického poľa. V tomto prípade môžeme využiť výsledky získané v odseku 8.1.6.1 a uplatniť princíp superpozície. Situáciu znázorňuje obr. 8.1.6.3.1. Prvá plocha je daná rovinou x = 0 a je na nej rozložený náboj s plošnou hustotou s . Druhá plocha je daná rovinou x = d a je na nej náboj s plošnou hustotou - s. Zaujímame sa o elektrické pole v okolí týchto plôch a medzi nimi. Pre polia blízko nabitej plochy použiť aproximáciu (8.1.6.1.7) Musíme pritom rozlišovať 3 oblasti:
a) x < 0, v tejto oblasti dostávame
![]() ,
, ![]()
![]()
a výsledné pole
![]() (8.1.6.3.1a)
(8.1.6.3.1a)
b) 0 < x < d, v tejto oblasti platí
![]() ,
, ![]()
![]()
čiže
![]() (8.1.6.3.1b)
(8.1.6.3.1b)
c) x > d
![]() ,
, ![]()
![]()
a
![]() (8.1.6.3.1c)
(8.1.6.3.1c)
Ak teda zanedbáme efekty spojené s okrajmi nabitých plôch, tak môžeme konštatovať: Elektrické polia od kladne a záporne nabitej plochy sa zvonka vyrušia. V priestore medzi dvoma plochami je homogénne elektrické pole veľkosti
![]()
