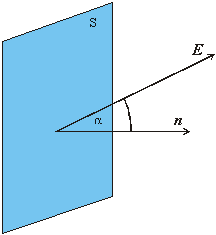
Obr.8.1.7.1.1

Definícia toku intenzity elektrického poľa

Pre elektrické a gravitačné polia je typický pokles intenzity poľa so štvorcom vzdialenosti od zdroja. Pre takéto polia je užitočné zaviesť novú veličinu – “tok intenzity poľa”. Budeme postupovať nasledovne. (Pozri obr. 8.1.7.1.1)

Zvolíme si malú orientovanú rovinnú plôšku S. Pod orientáciou plôšky rozumieme to, že sme si vybrali jednu z dvoch možností orientácie jednotkového normálového vektora n k rovine v ktorej sa nachádza táto plôška. Plôška S musí byť dostatočne malá tak, aby vektor E bol vo všetkých jej bodoch rovnaký. Tok intenzity elektrického poľa plochou S definujeme ako skalárnu veličinu - súčin veľkosti normálovej zložky vektora E a veľkosti plochy S

(8.1.7.1.1)

S takýmito výrazmi sa budeme odteraz stretávať často, preto sa niekedy zavádza i pojem plošného vektora, t.j. vektora, ktorý má smer normály n k danej ploche a dĺžka vektora je daná veľkosťou plochy S

S = nS (8.1.7.1.2)

V tomto texte však budeme vždy explicitne uvádzať normálový vektor n pri ploche S.

Vo všeobecnosti si môžeme zvoliť plochu S ako veľkú zakrivenú plochu a našu definíciu toku Y musíme vhodne zovšeobecniť. (Pozri obr. 8.1.7.1.2) Urobíme to tak, že celú plochu S rozdelíme na veľmi malé elementárne plôšky dS a pre každú nájdeme normálový vektor n. Potom vypočítame elektrické pole E v mieste každej plôšky, príspevok k toku intenzity poľa dY a všetky príspevky spočítame. Matematicky to vyjadríme takto

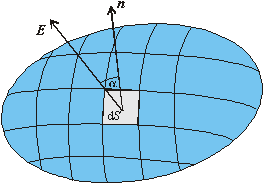
Obr.8.1.7.1.2

Tok elektrického poľa cez veľkú zakrivenú plochu

(8.1.7.1.3)

Tok elektrostatického poľa bodového náboja v špeciálnom prípade guľovej plochy

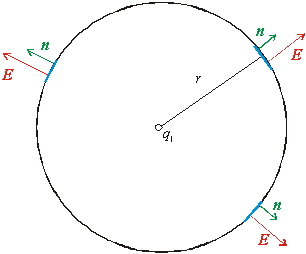
Obr.8.1.7.2.1

Tok elektrického poľa cez sférickú plochu okolo bodového náboja v počiatku

Zaujímavé výsledky dostaneme, ak budeme plochu S voliť ako spojitú, hladkú a uzavretú plochu. Najjednoduchší prípad predstavuje sférická plocha s polomerom r okolo kladného bodového náboja q₁, ktorý sa nachádza v začiatku súradnicovej sústavy (r₁ = 0). (Pozri obr. 8.1.7.2.1) Pri uzavretých plochách budeme zachovávať konvenciu, že normálový vektor n je vždy orientovaný zvnútra plochy von. V tomto prípade

(8.1.7.2.1)

a

(8.1.7.2.2)

Potom skalárny súčin E . n dáva

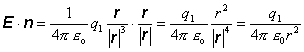(8.1.7.2.3)

Táto veličina je však pri pevnej hodnote polomeru r konštantná, takže pre výsledný tok intenzity poľa ihneď dostaneme

(8.1.7.2.4)

Dostali sme zaujímavý výsledok, ktorý sa pokúsime ďalej zovšeobecniť.