Tok elektrického poľa bodového náboja pri všeobecnom tvare plochy S

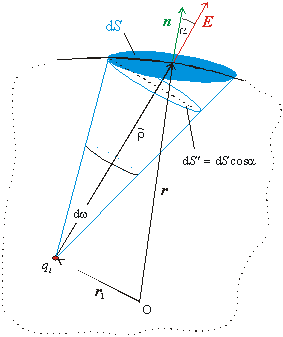
Obr.8.1.8.1.1

Plocha S okolo náboja q_i

Uvažujme celkom všeobecnú plochu S, ktorá obklopuje náboj q_i. Plochu rozdelíme na malé plôšky dS, v rozsahu ktorých je vektor poľa E konštantný. Ak každým okrajovým bodom plôšky dS vedieme priamku, ktorá prechádza bodovým nábojom q_i, tak dostaneme kužeľovú plochu, ktorá pri svojom vrchole definuje priestorový uhol dw.

Priestorový uhol w definujeme podľa analógie uhla v rovine ako podiel veľkosti plochy S na povrchu gule o polomere r, ktorú kužeľová plocha obopínajúca priestorový uhol w vytína, ku kvadrátu polomeru r. Plný priestorový uhol W vypočítame ako veľkosť povrchu gule s jednotkový polomerom, čiže W = 4p 1² = 4p. Príspevok od plôšky dS k toku elektrického poľa je

dY_i = E . n dS = E dS . cos a = dS´ (8.1.8.1.1)

súčin dS . cos a však môžeme interpretovať ako veľkosť priemetu plôšky dS do roviny, ktorá je kolmá na vektor r = r - r_i. Tento priemet sme označili ako dS´. Na základe definície priestorového uhla zrejme platí

(8.1.8.1.2)

alebo obrátene

dS´ = r²dw (8.1.8.1.3)

Pokiaľ má plocha S taký tvar, že každá polpriamka vychádzajúca z bodového náboja q_i ju pretína iba raz (v jedinom bode), tak normála n je orientovaná od náboja q_i a cosa je kladný. Potom sčítanie príspevkov od všetkých elementov dS je jednoduché

(8.1.8.1.4)

Vo všeobecnosti však musíme predpokladať zložitejší tvar plochy S a pri záhyboch tejto plochy sa budú vyskytovať príspevky, kde cosa bude mať ako kladné tak aj záporné hodnoty. Pozri obr.8.1.8.1.2.

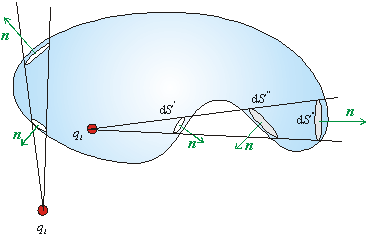
Obr.8.1.8.1.2

Príspevky od plošiek dS pri zložitom tvare plochy S

Pre jeden kužeľ obopínajúci uhol dw sú všetky príspevky E .dS´, E . dS´´, ...., čo do absolútnej hodnoty rovnaké, lebo r² v menovateli pre E sa vyruší s členom r² vo výraze dS´= r² dw. Znamienko takéhoto príspevku závisí od lokálnej orientácie normály n. Môžu nastať dva prípady:

1. Náboj q_i sa nachádza vo vnútri plochy S.

V mieste prvého príspevku k dY vektor r vychádza zvnútra plochy S von, normála n je orientovaná od náboja q_i a teda cosa > 0. V mieste ďalšieho príspevku E.n dS´´ už vektor r prechádza z vonkajšej strany plochy S dovnútra, normála n smeruje k náboju q_i a znamienko príspevku je záporné. Vektor r takto pretína plochu S v nepárnom počte bodov, a preto párny počet rovnakých príspevkov s opačnými znamienkami sa vyruší a do výsledku zostáva iba prvý z nich. Teda

(8.1.8.1.5)

2. Náboj q_i sa nachádza mimo plochy S

Zopakujeme tú istú úvahu ako v predchádzajúcom prípade. Rozdiel je len v tom, že vektor r pretína plochu S v párnom počte bodov, takže všetky príspevky k dY sa v konečnom dôsledku vyrušia a výsledok je rovný nule. Teda

(8.1.8.1.6)

Príklad 8.1.8

Dva náboje – 4.10^-7 C a 5.10^-7 C sú vo vzdialenosti 10 cm. Náboje sa nachádzajú vo vákuu.

a) Akou silou na seba pôsobia ?

b) Aký je tok vektora intenzity elektrostatického poľa cez plochu, ktorá obklopuje obidva tieto náboje?

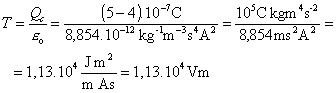
Tok intenzity elektrostatického poľa sústavy bodových nábojov - Gaussova veta

Výsledok, ktorý sme získali v predchádzajúcom odseku môžeme teraz zovšeobecniť na ľubovoľnú sústavu bodových nábojov q_i ( i = 1, 2, ..., n ). Podľa princípu superpozície je

(8.1.8.2.1)

a teda

Pritom do sčítavania sa započítavajú iba tie náboje, ktoré sa nachádzajú vo vnútri plochy S. Výsledok (8.1.8.2.2), ku ktorému sme sa dopracovali sa nazýva Gaussova veta elektrostatiky. (Existuje ešte Gaussova veta vo vektorovom počte) Gaussova veta predstavuje integrálny ekvivalent Coulombovho zákona. Slovami môžeme Gaussovu vetu formulovať takto:

Tok vektora intenzity elektrostatického poľa vo vákuu cez uzavretú plochu na vonkajšiu stranu sa rovná podielu celkového náboja uzavretého touto plochou a permitivity vákua e _o .

(8.1.8.2.2)

Gaussova veta je veľmi dôležitá nielen pre výpočty elektrických polí v prípadoch, kde s a dá výhodne využiť symetria rozloženia nábojov, ale ako dôležitý nástroj v teórii ektromagnetických polí.