 Spojité rozloženie náboja, výpočet elektrostatického poľa pomocou Gaussovej vety
Spojité rozloženie náboja, výpočet elektrostatického poľa pomocou Gaussovej vety
Elektrické pole nekonečnej nabitej roviny
Na ilustráciu ako sa riešia úlohy pomocou Gaussovej vety si urobíme výpočet elektrického poľa v blízkosti nabitej roviny. Situácia je znázornená na obr. 8.1.9.1.1.
Uvažujme plochu, ktorá obopína časť náboja v rovine. Výber plochy volíme tak, aby sme maximálne využili symetrie, ktoré sa v úlohe vyskytujú. V našom prípade ak je nabitá rovina dostatočne veľká a bod pozorovania P je ďaleko od okrajov roviny, tak vektor poľa E je orientovaný kolmo na rovinu. Preto je výhodné plochu S voliť ako povrch valca s osou kolmo na rovinu. Vtedy na povrchu plášťa valca bude vždy vektor poľa rovnobežný s povrchom - kolmá zložka na povrch je rovná nule a teda aj celý tok plášťom. Zostávajú iba dva príspevky od dna valca a jeho čela, kde je vektor poľa rovnobežný s normálou.
Y = E1 . S + E2 . S (8.1.9.1.1)
Úloha s nabitou rovinou sa vyznačuje zrkadlovou symetriou voči tejto rovine, z čoho vyplýva rovnosť veľkosti vektorov E1 a E2. Teda
E1 = E2 = E (8.1.9.1.2)
a
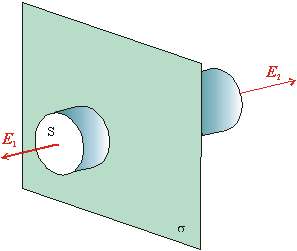
Obr.8.1.9.1.1
K výpočtu poľa nabitej roviny
Y = 2 E . S (8.1.9.1.3)
Potom podľa Gaussovej vety platí
![]() (8.1.9.1.4)
(8.1.9.1.4)
a teda
![]() (8.1.9.1.5)
(8.1.9.1.5)
Výsledok je zhodný s tým, čo sme dostali priamym výpočtom na osi kruhového disku tesne nad nabitou plochou disku. Vidíme, že výpočet podľa Gaussovej vety je oveľa jednoduchší a postup všeobecnejší, takže vzťah (8.1.9.1.5) platí aj pre konečné nabité rovinné plochy ďaleko od okrajov a aj pre polia tesne u zakrivených nabitých plôch s veľkým polomerom krivosti.
Príklad 8.1.9.1.1
Akou silou je priťahovaná kladne nabitá častica s nábojom q k záporne nabitej nekonečne veľkej rovine s plošnou hustotou náboja s- Náboje sa nachádzajú vo vákuu. q = 4,8 mC, ÷s-÷ = 2 mCm-2
Riešenie
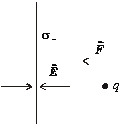
Obr.8.1.9.2
Intenzita v okolí veľkej roviny je
![]()
![]()
Príklad 8.1.9.1.2
Dve kovové platne s plochami 100 cm2 sú vo vzdialenosti 2 cm. Na ľavej platni je náboj – 2.10-9 C a na pravej náboj + 2.10-9 C. Vypočítajte príťažlivú silu, ktorou jedna platňa pôsobí na druhú. Platne sa nachádzajú vo vákuu.
q1 = - 2.10-9 C
q2 = + 2.10-9 C
S = 100 cm2 = 1. 10-2 m2
a = 2 cm = 2. 10-2 m
Riešenie
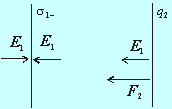
Obr.8.1.9.2
Náboj q1 je na ľavej platni rozložený rovnomerne s plošnou hustotou
![]()
Takýto náboj budí v blízkosti povrchu nabitej roviny elektrické pole intenzity
![]()
Vektor intenzity E1 smeruje k doske nabitej nábojom q1 . Pri zanedbaní okrajových efektov na krajoch dosky, E1 nezávisí na vzdialenosti od dosky. Výsledná sila pôsobiaca na náboj q2 je
![]()
Keďže náboj q2 je kladný, tak sila F2 má rovnaký smer ako intenzita poľa E1 , a preto sa dosky budú priťahovať. Číselne pre veľkosť tejto sily dostaneme:
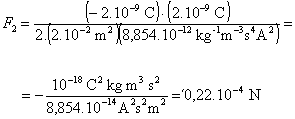
Elektrické pole rovnomerne nebitej gule
Máme guľu (sféru) s polomerom R, ktorá je rovnomerne nabitá elektrickým nábojom s objemovou hustotou r. Situáciu znázorňuje obr. 8.1.9.2.1. Pre tento prípad je typická sférická symetria úlohy, t.j. že pri otočení systému okolo ľubovoľnej osi prechádzajúcej stredom gule sa žiadna fyzikálna veličina nemení. Z toho vyplýva, že:
· elektrické pole má radiálny smer
· veľkosť vektora E t.j. E = |E | je funkciou iba vzdialenosti r od stredu gule.
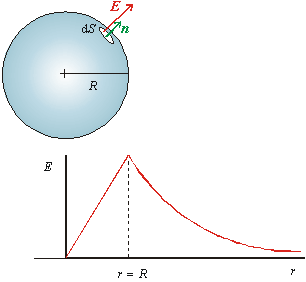
Obr. 8.1.9.2.1
Výpočet elektrického poľa rovnomerne nabitej gule.
V tomto prípade je najvýhodnejšie zvoliť plochu S ako sférickú plochu o polomere r. Potom pole E na povrchu plochy je v každom bode rovnobežné s normálou n k ploche S. Tok elektrického poľa potom ľahko dostaneme
![]() (8.1.9.2.1)
(8.1.9.2.1)
Náboj q, ktorý je takouto plochou obklopený závisí od polomeru r. Ak je r < R, tak vo vnútri plochy sa nachádza iba časť náboja celého telesa
![]() (8.1.9.2.2)
(8.1.9.2.2)
Z Gaussovej vety potom vyplýva
![]() (8.1.9.2.3)
(8.1.9.2.3)
z čoho po úprave dostaneme
![]() pre r < R (8.1.9.2.4)
pre r < R (8.1.9.2.4)
Pre plochy S, kde r > R je náboj vo vnútri plochy konštantný
![]() , (8.1.9.2.5)
, (8.1.9.2.5)
takže pre výsledné pole dostaneme
![]() r > R (8.1.9.2.6)
r > R (8.1.9.2.6)
Priebeh veľkosti vektora intenzity poľa E je znázornený na obr. 8.1.9.2.1. Vidíme, že veľkosť vektora od stredu gule najprv lineárne vzrastá. Najväčšiu hodnotu dosahuje na povrchu gule. Elektrické pole mimo nabitej gule klesá so štvorcom vzdialenosti. Výsledok je dôležitý aj z toho hľadiska, že pole rovnomerne nabitej gule v priestore mimo nej je presne také isté ako pole bodového náboja umiestneného v jej strede, rovnakej veľkosti ako je celkový náboj gule. Toto do istej miery oprávňuje aproximáciu nabitých telies bodovými nábojmi.
Elektrické pole gule nabitej iba na povrchu
Uvažujme dutú sféru s polomerom R, ktorá nesie na povrchu elektrický náboj s plošnou hustotou s. Situáciu znázorňuje obr. 8.1.9.3.1. Dutosť telesa (gule) predpokladáme z toho dôvodu, aby sme sa vyhli vzájomnému pôsobeniu náboja na povrchu gule s nábojmi v látke, z ktorej je teleso. Je to zložitý problém, ktorému sa budeme venovať až v ďalšej kapitole.
Budeme postupovať podobne ako v predchádzajúcom prípade. Stred súradnicovej sústavy umiestnime do stredu gule. Pre úlohu je typická sférická symetria, z čoho vyplýva radiálny smer vektora E. Jeho veľkosť E je potom funkciou iba vzdialenosti r od stredu.
Plochu S budeme voliť ako sférickú plochu o polomere r. Na tejto sférickej ploche je potom vektor E vždy rovnobežný s miestnou normálou n a pre tok elektrostatického poľa dostaneme
![]() (8.1.9.3.1)
(8.1.9.3.1)
Teraz musíme rozlišovať dva prípady r < R a r > R. Ak r < R, tak vo vnútri gule nie je žiaden elektrický náboj, a preto tok Y = 0. Z toho ihneď vyplýva
E = 0 , ak r < R (8.1.9.3.2)
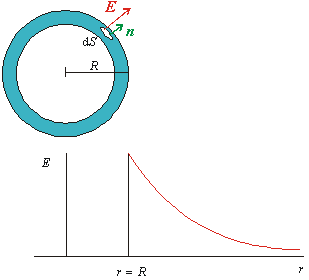
Obr. 8.1.9.3.1
Výpočet elektrického poľa gule nabitej na povrchu
V druhom prípade, ak r > R, tak vo vnútri plochy S sa nachádza všetok náboj, ktorý je na povrchu nabitej gule, takže podľa Gaussovej vety platí
![]() (8.1.9.3.3)
(8.1.9.3.3)
z čoho vyplýva
![]() , ak r > R (8.1.9.3.4)
, ak r > R (8.1.9.3.4)
Závislosť intenzity poľa od vzdialenosti r od stredu gule je znázornená na obr. 8.1.9.3.1.
Na funkčnej závislosti E(r) nás prekvapuje nespojitosť v bode r = R. Tu si znova musíme pripomenúť, že sme pracovali s abstrakciou gule, kde sa náboj na povrchu rozkladá v nekonečne tenkej vrstve. V skutočnosti, ak máme teleso nabité na povrchu, tak tento elektrický náboj sa vždy rozprestiera vo vrstve konečnej hrúbky. Výpočty ukazujú, že napríklad v kovoch hrúbka takejto vrstvy predstavuje niekoľkých atomárnych rovín, čo je však z makroskopického hľadiska zanedbateľná hrúbka. V rozsahu takejto veľmi tenkej vrstvy potom elektrické pole spojito narastá z nuly na konečnú hodnotu tesne nad povrchom ( E(R) = s / eo)
Elektrostatické pole nekonečne dlhého nabitého vlákna
Uvažujeme nekonečne dlhé vlákno s elektrickým nábojom s konštantnou dĺžkovou hustotou l. Pri riešení využijeme valcovú symetriu, ktorá je typická pre tento problém. To znamená, že elektrické pole nemá zložky rovnobežné s osou vlákna, ale v každom bode je vektor E kolmý na os vlákna. Situáciu znázorňuje obr.8.1.9.4.1. Okrem toho situácia je nezmenená pri ľubovoľnom pootočení okolo osi vlákna, z čoho vyplýva, že v rovnakej vzdialenosti a od vlákna majú všetky vektory E rovnakú veľkosť. Teda E = |E | závisí iba od a.
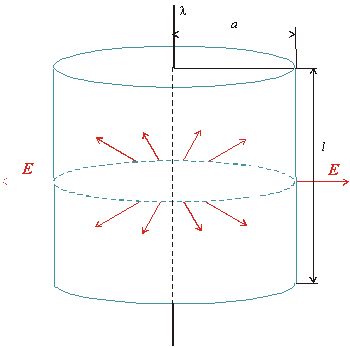
Obr. 8.1.9.4.1
Výpočet elektrického poľa nekonečne dlhého nabitého vlákna
V tomto prípade je výhodné voliť plochu S ako valcovú plochu s polomerom a a výškou l súosú s nabitým vláknom. Vo všetkých bodoch čela a dna tejto plochy je vektor poľa E kolmý na miestnu normálu k ploche dS, takže príspevok k toku intenzity poľa je nulový. Nenulový príspevok dostaneme iba od plášťa valca, kde je vektor E v každom bode rovnobežný s normálou n. Okrem toho vektory E majú na tomto plášti rovnakú veľkosť, takže
![]() (8.1.9.4.1)
(8.1.9.4.1)
Z toho ihneď máme pre intenzitu poľa E vo vzdialenosti a od vlákna
![]() (8.1.9.4.2)
(8.1.9.4.2)
