 Približné vyjadrenie potenciálu a elektrostatického poľa sústavy nábojov
Približné vyjadrenie potenciálu a elektrostatického poľa sústavy nábojov
V tomto odseku sa budeme zaoberať približným vyjadrením potenciálu a vektora intenzity elektrického poľa sústavy elektrických nábojov. V praxi sa totiž často vyskytuje situácia, že elektrické náboje sú lokalizované v malej oblasti priestoru a nás zaujíma potenciál a elektrické pole iba vo väčšej vzdialenosti od takejto oblasti. Tento postup si najprv ukážeme na najjednoduchšej sústave nábojov - elektrickom dipóle a potom ho zovšeobecníme.
Elektrický dipól
Uvažujme dva bodové náboje rovnako veľké, ale opačného znamienka, ktoré sú umiestnené blízko seba. Situácia je znázornená na obr. 8.1.11.1.1. Takúto sústavu nábojov nazývame elektrickým dipólom.
Začiatok súradnicovej sústavy umiestnime do stredu medzi oboma nábojmi. Os z budeme voliť v smere spojnice týchto nábojov. Vzdialenosť medzi nábojmi označíme ako a. Polohový vektor kladného náboja q+ označíme ako a+, polohový vektor záporného náboja q- je a- . Pre potenciál tejto sústavy nábojov zrejme platí
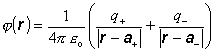 (8.1.11.1.1)
(8.1.11.1.1)
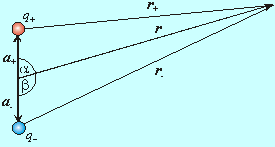
Obr.8.1.11.1.1
Elektrický dipól.
Ako sme už zdôraznili, zaujíma nás potenciál a pole v oblasti, kde
![]() (8.1.11.1.2)
(8.1.11.1.2)
Všimnime si, ako sa dá na základe tejto podmienky upraviť výraz
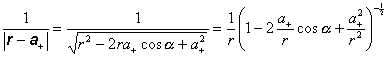 (8.1.11.1.3)
(8.1.11.1.3)
Druhý a tretí člen v zátvorke sú veličiny veľmi malé oproti 1. V takom prípade sa dá na mnohočlen v zátvorke aplikovať "zovšeobecnená binomická veta"
![]() (8.1.11.1.4)
(8.1.11.1.4)
ak |e|<< 1 a "binomické" koeficienty počítame podľa známeho vzťahu bez ohľadu na to, že r je racionálne číslo
![]() (8.1.11.1.5)
(8.1.11.1.5)
Exaktne možno vzťah (8.1.11.1.5) odvodiť rozvinutím výrazu na ľavej strane (8.1.11.1.4) do Taylorovho rozvoja v okolí e = 0. Formula (8.1.11.1.4) je veľmi užitočná pri rôznych fyzikálnych úvahách, nakoľko nám umožňuje postupovať systematicky pri zanedbávaní malých veličín. V našom prípade sa obmedzíme iba na veličiny prvého rádu, teda a+/r a všetky vyššie mocniny budeme zanedbávať. Tým dostaneme
![]() (8.1.11.1.6)
(8.1.11.1.6)
Podobne dostaneme
![]() (8.1.11.1.7)
(8.1.11.1.7)
kde sme využili vlastnosť funkcie kosínus
cosb = cos(p-a) = - cosa (8.1.11.1.8)
Tým pre výsledný potenciál dostaneme vzťah
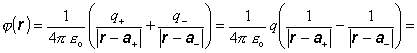
![]() (8.1.11.1.9)
(8.1.11.1.9)
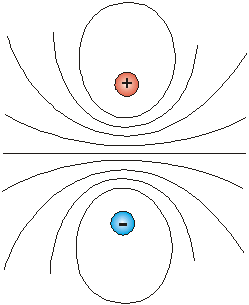
Obr. 8.1.11.2
Vidíme, že vo väčších vzdialenostiach r od dipólu jeho potenciál klesá s druhou mocninou tejto vzdialenosti. Možno očakávať, že elektrické pole bude potom klesať s treťou mocninou vzdialenosti r. Toto nie je v rozpore s Coulombovým zákonom, nakoľko vzťah (8.1.11.1.9) predstavuje približný výraz pre potenciál. Priebeh ekvipotenciálnych hladín elektrického dipólu je znázornený na obr. 8.1.11.2
Potenciál a elektrické pole sústavy nábojov vo väčšej vzdialenosti
Postup uvedený v predchádzajúcom odseku môžeme zovšeobecniť na ľubovoľnú sústavu nábojov, ktorá je obmedzená na malú oblasť priestoru a potenciál budeme počítať mimo tejto oblasti. Počiatok súradnicovej sústavy umiestnime do tejto oblasti. V bodoch určených polohovými vektormi a1, a2,… an sa nachádzajú náboje q1, q2, ..., qn. Pozri obr. 8.1.11.3.
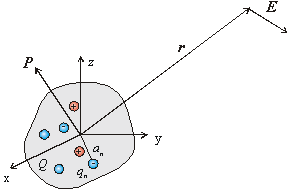
Obr. 8.1.11.3
Sústava bodových nábojov
Potenciál sústavy v bode r je
![]() (8.1.11.2.1)
(8.1.11.2.1)
Vo väčších vzdialenostiach od tejto sústavy je ai/r << 1. Potom platí
![]() (8.1.11.2.2)
(8.1.11.2.2)
Výraz aicosai môžeme vyjadriť cez skalárny súčin vektora ai a polohového vektora r
![]() (8.1.11.2.3)
(8.1.11.2.3)
Potom pre celkový potenciál dostaneme
![]() (8.1.11.2.4)
(8.1.11.2.4)
Vidíme, že potenciál j sa skladá z dvoch členov. Prvý obsahuje súčet všetkých nábojov sústavy
![]()
a klesá s 1. mocninou vzdialenosti r. Druhý člen obsahuje vektorový súčet výrazov qi ai, ktorý budeme označovať ako celkový “dipólový moment” sústavy nábojov
![]() (8.1.11.2.5)
(8.1.11.2.5)
Výsledný potenciál sústavy je
![]() (8.1.11.2.6)
(8.1.11.2.6)
Keby sme v našom priblížení akceptovali aj vyššie mocniny ai/r dostali by sme ďalšie členy, ktoré odpovedajú vyšším momentom charakterizujúcim rozloženie náboja (kvadrupól, oktupól atd.). Derivovaním výrazu (8.1.11.2.6) dostaneme ihneď vyjadrenie pre intenzitu elektrického poľa sústavy
![]()
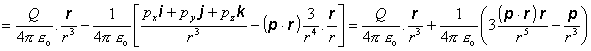 (8.1.11.2.7)
(8.1.11.2.7)
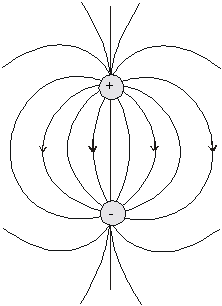
Obr. 8.1.11.4
Siločiary elektrostatického poľa dipólu.
Často sa stáva, že výsledný elektrický náboj sústavy Q je rovný nule - sústava (teleso) je elektricky neutrálna, avšak vo výraze pre pole zostáva príspevok od dipólového momentu p
![]() (8.1.11.2.8)
(8.1.11.2.8)
Ak zvolíme osi súradnicovej sústavy tak, aby os z bola rovnobežná so smerom dipólo-vého momentu p, potom p = pk a
![]() (8.1.11.2.9)
(8.1.11.2.9)
![]() (8.1.11.2.10)
(8.1.11.2.10)
Siločiary elektrostatického poľa dipólu sú znázornené na obr. 8.1.11.4.
