Radiálny charakter elektrostatického poľa a jeho matematické vyjadrenie

Vráťme sa teraz k príkladu s rovnomerne nabitou guľou o polomere R. Vo vnútri gule má elektrické pole E radiálny smer a jeho veľkosť lineárne vzrastá s polomerom r, teda

(8.1.12.1.1)

V úvodnej kapitole vektorového počtu bola popri gradient skalárnej funkcie zavedená operácia divergencie vektorovej funkcie. Skúsme teraz vypočítať divergenciu z poľa E vo vnútri gule

(8.1.12.1.2)

Mimo nabitej oblasti gule r > R má pole E tvar

(8.1.12.1.3)

Vypočítajme divergenciu z tohoto výrazu:

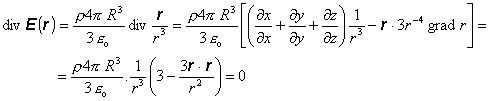(8.1.12.1.4)

Dospeli sme k celkom zaujímavému výsledku:

· V miestach, kde je náboj rozložený spojito s konštantnou hustotou r je

(8.1.12.1.5)

· V miestach, kde nie je náboj

(8.1.12.1.6)

Vzťah (8.1.12.1.5) súvisí s našou konvenciou definície siločiar elektrického poľa. Povedali sme, že siločiary vychádzajú z miesta kladného náboja a vstupujú do miesta, kde je záporný náboj. To znamená, že všade tam, kde sa nachádzajú nové náboje vznikajú nové siločiary. Týchto siločiar je tým viac čím viac nábojov sa v danom mieste nachádza, t.j. čím je väčšia hustota náboja v danom bode. Presne toto vyjadruje aj rovnica (8.1.12.1.5). Vo voľnom priestore, kde nie sú žiadne náboje je div E = 0. Vidíme, že veličina div E nám znázorňuje vytekanie vektora elektrického poľa všade z tých miest, kde sa nachádzajú náboje.

I. Maxwellova rovnica pre vákuum

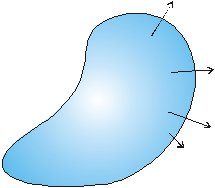
Pokúsime sa teraz zistiť, či tento výsledok platí celkom všeobecne. Uvažujme nejaký objem V ohraničený uzavretou plochou S. V ňom sa nachádza elektrický náboj, ktorý je spojito rozložený s objemovou hustotou r. Situáciu znázorňuje obr.8.1.12.1.

Podľa Gaussovej vety platí

(8.1.12.2.1)

V prvej kapitole vo vektorovom počte sme sa dozvedeli, že za istých podmienok (diferencovateľnosť funkcií, hladká plocha atd.) je možné plošný integrál previesť na objemový. Platí

(8.1.12.2.2)

kde V je objem uzavretý plochou S. Tento matematický vzťah sa v literatúre nazýva Gauss-Ostragradského veta, alebo Gaussova veta vektorového počtu. Ak aplikujeme túto matematickú transformáciu na ľavú stranu rovnice (8.1.12.2.1), tak dostaneme

(8.1.12.2.3)

Rovnicu môžem prepísať nasledovne

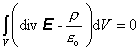(8.1.12.2.4)

Pritom plochu S, resp. objem V, ktorý je ňou ohraničený možno voliť celkom ľubovoľne. To ale znamená, že integrand v rovnici (8.1.12.2.4) musí byť identický rovný nule. Nie je totiž možné, aby integrand bol v jednej časti priestoru kladný a inde záporný a tým by sa príspevky k integrálu kompenzovali, lebo už pri malej zmene objemu V by rovnica potom prestala platiť. Tým dostávame elegantný výsledok

(8.1.12.2.5)

Toto je prvá Maxwellova rovnica pre elektrostatické pole vo vákuu. Rovnica hovorí, že divergencia intenzity elektrického poľa sa rovná podielu hustoty náboja a permitivity vákua.

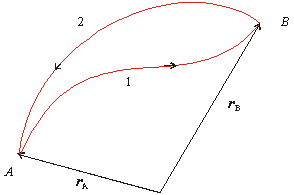
Pre elektrostatické pôsobenie nábojov je typický centrálny charakter elektrických síl. V dôsledku toho má vektor poľa radiálny smer a vďaka tomu sme mohli zaviesť elektrický potenciál. Skúsme teraz vytvoriť dve rôzne integračné cesty medzi bodmi A, B.

V elektrostatickom poli platí

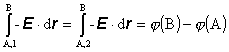(8.1.12.2.6)

Vytvorme teraz uzavretú integračnú cestu C = A ® 1 ® B ® 2 ® A. Zrejme platí

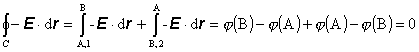(8.1.12.2.7)

Keby rovnica (8.1.12.2.7) neplatila, vedeli by sme nájsť takú cestu v elektrickom poli, že po každom obehu by sme získali určitú energiu, čo by bolo v rozpore so zákonom zachovania energie. Na druhej strane integrál z vektorovej funkcie po uzavretej krivke možno podľa Stokesovej vety transformovať na plošný integrál, takže

(8.1.12.2.8)

Ak uvážime, že krivka C je celkom ľubovoľná, tak rovnica (8.1.12.2.8) bude splnená iba tak, že jej integrand sa identický rovná nule, čiže

rot E = 0 (8.1.12.2.9)

Rovnica (8.1.12.2.9) predstavuje špeciálny prípad 4. Maxwellovej rovnice pre statické pole E. Rovnica ukazuje, že elektrostatické pole nemá vírový charakter. Rovnice (8.1.12.2.5) a (8.1.12.2.9) úplne popisujú všetky elektrostatické javy vo vákuu. Na týchto rovniciach sa najlepšie odzrkadľuje nová kvalita popisu elektromagnetických javov prostredníctvom veličín poľa. Zmeny elektrického poľa v okolí nejakého bodu závisia iba od lokálnej hustoty elektrického náboja.

 

Kontrolné otázky