Majme kondenzátor kapacity C nabitý nábojom Q na napätie U. Ako bolo ukázané v časti 8.1.10, elektrostatické pole je schopné konať prácu pri premiestňovaní náboja . Pokiaľ by náboj v kondenzátore mohol prechádzať z jednej dosky na druhú, elektróny by boli poľom urýchlené, získali by kinetickú energiu (pokiaľ by sa táto nepremenila odporom vedenia na teplo), kondenzátor by sa vybil, pole medzi doskami by vymizlo. V súlade so zákonom zachovania energie musí mať elektrostatické pole energiu W, ktorá sa pri vybíjaní kondenzátora premení na inú formu. Je zrejmé, že táto energia sa musí rovnať práci na nabitie pôvodne nenabitého kondenzátora, to znamená na postupné prenesenie kladného náboja z dosky zápornej na kladnú. Na prenesenie prvého elementárneho kladného náboja dQ⁺ nie je potrebná práca, tento však vytvorí medzi doskami kondenzátora elektrostatické pole. Pri prenášaní ďalšieho náboja dQ⁺ už proti pohybu pôsobí sila elektrostatického poľa. Ak je kondenzátor už nabitý nábojom dQ⁺ na napätie U, je na prenesenie náboja dQ⁺ potrebná práca

.

Celá práca potrebná na nabitie pôvodne nenabitého kondenzátora, to znamená na postupné prenesenie celého náboja Q na kladnú dosku, je

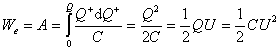. (8.4.4.1)

Podobný vzťah by sme dostali aj v prípade, že by sme nabíjali osamelý vodič, prenášaním náboja z veľkej vzdialenosti na vodič. V tom prípade napätie U je v skutočnosti konečný potenciál V , ktorý by mal vodič po nabití nábojom Q:

(8.4.4.2)

Tento vzťah je zhodný zo vzťahom (8.4.3.3) pre sústavu nábojov, všetky čiastkové náboje sú na potenciáli vodiča V a ich súčet je Q.