Hustota energie elektrického poľa
Počítajme energiu nabitého doskového kondenzátora. Predpokladajme, že rozmery dosiek sú veľké v porovnaní so vzdialenosťou dosiek, medzi doskami je dielektrikum permitivity e. Potom môžeme predpokladať, že pole medzi doskami je homogénne a je vytvorené len v objeme t medzi doskami kondenzátora. Za predpokladu homogénneho poľa je
,
kde E je intenzita tohoto poľa a d vzdialenosť dosiek kondenzátora. Kapacita doskového kondenzátora je daná vzťahom (8.4.2.1), kde S je obsah plochy dosky. Potom po dosadení do vzťahu (8.4.4.1) dostávame a s ohľadom na (8.3.5.1)
,
kde 
je objem homogénneho poľa v kondenzátore. Energiu pripadajúcu na jednotku objemu nazveme hustotou energie elektrostatického poľa we
. (8.4.5.1)
Tento vzťah sa dá zovšeobecniť aj pre pole nehomogénne. Ako bolo povedané v časti (8.3.6) v anizotropnom dielektriku nemá vektor elektrostatickej indukcie rovnaký smer ako vektor intenzity elektrostatického poľa. V takýchto poliach platí všeobecnejší vzťah
. (8.4.5.2)
Energia elektrostatického poľa je skutočne rozložená v priestore, kde sa nachádza pole, toto pole je schopné konať prácu, urýchľovať v ňom sa nachádzajúce nabité častice. U premenného elektromagnetického poľa ako je napr. svetlo nám vôbec nenapadne jeho energiu spájať s nejakým nábojom, ktorý ho vytvoril.
Príklad 8.4.1 Tri vodivé rovinné rovnaké dosky sú uložené paralelne vo vzdialenostiach d . Vypočítajte kapacitu kondenzátora, ktorý vytvoríme spojením krajných dosiek, druhou doskou kondenzátora je stredová doska
Riešenie
Sústavu si môžeme predstaviť ako keby stredná doska bola tvorená dvomi doskami priloženými k sebe, čo vlastne zväčšuje plochu dosiek kondenzátora na dvojnásobnú a podľa vzťahu 8.4.4 bude výsledná kapacita
Príklad 8.4.2 Vypočítajte kapacitu paralelne zapojených kondenzátorov a aplikujte tento výsledok na prípad rovinného doskového kondenzátora s plošným obsahom dosiek S =100 cm2 , ktorých vzdialenosť je d = 2 mm, ak zvislé dosky sú ponorené do etylalkoholu s relatívnou permitivitou er= 26 do jednej tretiny svojej plochy.
Riešenie
Dva paralelne zapojené kondenzátory môžeme považovať za jeden kondenzátor a jeho kapacitu určiť z definície. Priveďme náboj Q na dosky z jednej strany kondenzátorov, potom výsledná kapacita sústavy je
,
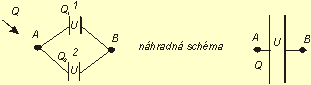
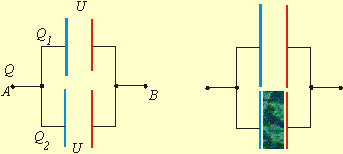
Obr. 8.4.2
kde U je napätie medzi bodmi A a B (obr.8.4.2). Náboj Q sa rozloží tak, aby obe dosky (navzájom spojené) mali rovnaký potenciál. Potom napätie na obidvoch kondenzátoroch bude rovnaké a platí
V prípade, že časť kondenzátora je vyplnená dielektrikom možno nahradiť dvomi kondenzátormi, jedným vákuovým a jedným z dielektrikom, s plošnými obsahmi dosiek tretina a dve tretiny z celkovej plochy:
Príklad 8.4.3 Urobte odhad „polomeru“ elektrónu za predpokladu, že je to guľa a jej pokojová energia E = mc2, (kde hmotnosť elektrónu m = 9 . 10-31 kg, rýchlosť svetla c = 3 . 108 m. s-1 ) je rovná energii vytvoreného elektrického poľa!
Riešenie
Energia elektrického poľa nabitého telesa je daná vzťahom 8.4.8:
.
Ak si potenciál vyjadríme pomocou kapacity
,
kde kapacita vodivej gule s polomerom R je
(podľa vzťahu 8.4.2) pre energiu poľa elektrónu dostávame
a z porovnania pokojovej energie hmotnosti m
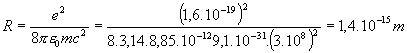
Príklad 8.4.4 Pomocou Kirchhoffových váh vyjadrite permitivitu kvapalného prostredia vloženého medzi dosky kondenzátora týchto váh! Kirchhoffove váhy tvorí kondenzátor umiestnený na váhy tak, že umožňuje merať elektrickú silu, ktorou je priťahovaná pohyblivá doska kondenzátora, ak tento je nabitý na napätie U. Usporiadanie váh podľa obr.(8.4.1) (zavesená pohyblivá kruhová doska plošného obsahu S je spojená vodivo s obkolesujúcim medzikružím) umožňuje predpokladať, že elektrické pole v kondenzátore je homogénne. Vzdialenosť pohyblivej dosky od druhej pevnej dosky je d.
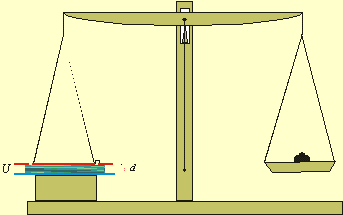
Obr. 8.4.1
Kirchoffove váhy
Riešenie
Vyvážime váhy nenabitého kondenzátora. Potom ho nabijeme na napätie U a novým vyvážením odmeriame silu F. Tuto silu vyjadríme zo zmeny energie elektrického poľa pri zmene vzdialenosti dosiek. Energiu dostaneme prenásobením hustoty energie (8.4.9) objemom kondenzátora
kde x je vzdialenosť dosiek. Pre silu dostávame
Intenzitu poľa vyjadríme zo zmeraného napätia ak vzdialenosť dosiek je d.
Potom platí
a pre hľadanú permitivitu prostredia
Poznámka: Vzťah pre silu je v zhode so skutočnosťou, že sila medzi nábojmi vložení do prostredia s relatívnou permitivitou er klesá er krát. Ak si energiu vyjadríme pomocou kapacity a náboja na jej doske, pre silu pôsobiacu na dosku kondenzátora dostávame
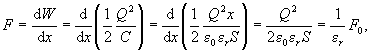
kde F0 je sila v prípade, že medzi doskami nie je dielektrikum.
Kontrolné otázky
- Ako sa zmení kapacita doskového kondenzátora, ak priestor medzi doskami vyplníme nevodivým olejom?
- Prečo môže byť kapacita kondenzátora podstatne väčšia ako kapacita osamelého vodiča?
- Vysvetlite čo je to energia elektrického poľa?
- Prečo zavádzame pojem hustota energie a aký má význam?
