Elektromagnetické pole je forma hmoty, ktorá má dve zložky - pole elektrické a pole magnetické. Rozdelenie elektromagnetického poľa na jeho dve zložky - pole elektrické a pole magnetické - je relatívne, to znamená, že závisí od podmienok, pri ktorých elektromagnetické pole pozorujeme pomocou prístrojov. V okolí nehybných nabitých telies pozorujeme silové pôsobenie elektrického poľa na nehybné skúšobné nabité teleso, ale nespozorujeme žiadne silové pôsobenie magnetického poľa na zmagnetizovanú nenabitú ihlu (magnetku) nehybného kompasu. Avšak ak sa súčasne iný pozorovateľ pohybuje spolu s kompasom vzhľadom na tieto nabité telesá, spozoruje silové pôsobenie magnetického poľa na magnetku svojho kompasu. Tento pozorovateľ to objasní tak, že magnetické pole je vyvolané pohybom elektrického náboja.

Z druhej strany, v okolí permanentných (trvalých) magnetov pozorujeme silové pôsobenie magnetického poľa na nenabitú magnetku nehybného kompasu, ale nepozorujeme silové pôsobenie na nehybné elektricky nabité teleso. Avšak ak sa súčasne iný pozorovateľ pohybuje spolu s nabitým telesom vzhľadom na tieto permanentné magnety, spozoruje silové pôsobenie na toto nabité teleso. Tento pozorovateľ to objasní tak, že sa magnetické pole mení v dôsledku pohybu trvalých magnetov vzhľadom na neho, a časovo premenlivé magnetické pole vyvolá v tom istom priestore indukované elektrické pole pôsobiace na nabité teleso. Ukazuje sa, že tiež časovo premenlivé elektrické pole vyvolá v tom istom priestore indukované magnetické pole.

Nakoniec, každý bod priestoru môže ľubovoľný pozorovateľ charakterizovať dvoma vektorovými veličinami, ktoré určujú výslednú silu pôsobiacu na elektrický náboj q. Zložkami výslednej elektromagnetickej sily sú elektrická sila F_e, ktorá nezávisí od rýchlosti elektrického náboja vzhľadom na pozorovateľa a magnetická sila F_m, ktorá závisí od vektora rýchlosti v elektrického náboja vzhľadom na pozorovateľa. Pomocou elektrickej sily F_e pôsobiacej na nehybný elektrický náboj q pozorovateľ definuje intenzitu elektrického poľa E

(10.1.1.1)

Pomocou magnetickej sily F_m pozorovateľ definuje vektorovú veličinu magnetická indukcia B

(10.1.1.2)

Jednotkou magnetickej indukcie B je zrejme (newton.sekunda)/(coulomb.meter). Používa sa kratší názov tesla (1 T) na počesť amerického elektrotechnika chorvátskeho pôvodu Nikolu Teslu (1856-1943). Magnetické pole s magnetickou indukciou B veľkosti 1 T pôsobí na elektrický náboj 1 C, ktorý sa pohybuje kolmo na vektor B rýchlosťou 1 m/s, silou 1 N.

Vzťahom (10.1.1.2) je magnetická indukcia B definovaná jednoznačne. Ak je elektrický náboj q kladný, magnetická sila F_m má ten istý smer ako vektorový súčin v ´ B, v prípade záporného náboja má smer opačný. Vektorový súčin v ´ B je kolmý na vektory v i B, jeho smer určujeme pravidlom pravej ruky (pravotočivej skrutky): ak zahnuté prsty pravej ruky ukazujú smer otočenia vektora v na vektor B cez menší z oboch uhlov, ktoré tieto dva vektory zvierajú, vztýčený palec ukazuje smer vektorového súčinu v ´ B. V smere palca by pri takom otočení postupovala pravotočivá skrutka. Pre veľkosť F_m magnetickej sily platí

(10.1.1.3)

kde j je uhol medzi smermi vektorov v a B s veľkosťami v a B (0 £ j £ p).

Celková elektromagnetická sila pôsobiaca na elektrický náboj q je superpozíciou elektrickej a magnetickej sily a nazývame ju podľa holandského fyzika Hendrika Antoona Lorentza (1853-1928) Lorentzova sila

(10.1.1.4)

Príklad 10.1.1.1

Elektrón bol z pokojového stavu urýchlený napätím 200 V. Aký je polomer kružnice a frekvencia pohybu elektrónu po kružnici po zapnutí homogénneho magnetického poľa s magnetickou indukciou veľkosti B = 1 mT? Rovina kružnice je kolmá na magnetickú indukciu B. Elektrický náboj elektrónu je q = -1,602.10^-19 C, hmotnosť elektrónu je m= 9,11.10^-31 kg. Relativistickú závislosť hmotnosti elektrónu od rýchlosti zanedbajte!

Riešenie

Elektrický náboj q urýchlený napätím U zvýši svoju kinetickú energiu o hodnotu êq êU. Počiatočná rýchlosť elektrónu bola nulová, preto s využitím vzťahu pre kinetickú energiu klasickej častice dostaneme

(10.1.1.1.1)

a po úprave pre veľkosť obvodovej rýchlosti dostaneme

(10.1.1.1.2)

Uhol j medzi smerom rýchlosti v a smerom magnetickej indukcie B je 90°, preto sa pravá strana vzťahu (10.1.1.3) zjednoduší. Pri uvedenom spôsobe pohybu úlohu dostredivej sily F zohráva magnetická sila F_m, preto porovnaním ich veľkostí dostaneme

(10.1.1.1.3)

 

a po úprave s využitím (10.1.1.1.1) získame vzťah pre polomer r kružnice

(10.1.1.1.4)

Perióda T je doba potrebná na jeden obeh kružnice

Frekvencia f je prevrátená hodnota periódy T

(10.1.1.1.5)

Perióda T a ani frekvencia f od rýchlosti elektrónu nezávisia, preto je možné striedavým napätím tejto frekvencie urýchľovať elektrón po rozvíjajúcej sa špirálovitej trajektórii v cyklotróne. Po dosadení zadaných hodnôt do vzťahov (10.1.1.1.4), (10.1.1.1.5) dostaneme

Polomer kružnice je 47,69 mm, frekvencia pohybu elektrónu po kružnici je 2,799.10⁷ s^-1.

Poznámka:

Podľa relativistickej fyziky, založenej na princípoch formulovaných Albertom Einsteinom (1879-1955), relativistická hmotnosť telesa (častice) m_r závisí od veľkosti rýchlosti v telesa (častice) vzhľadom na pozorovateľa podľa vzťahu

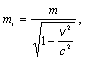(10.1.1.1.6)

kde c = 3.10⁸ m/s je rýchlosť svetla vo vákuu, m je hmotnosť telesa (častice), ktorá sa v minulosti nazývala tiež pokojová alebo kľudová hmotnosť. Kinetická energia E_k relativistickej častice je rozdielom relativistickej energie m_rc² a „pokojovej“ energie mc²

(10.1.1.1.7)

Dosadením (10.1.1.1.7) do pravej strany (10.1.1.1.1) a s využitím (10.1.1.1.6) po úpravách získame vzťah pre výpočet rýchlosti relativistickej častice. Na ľavej strane (10.1.1.1.3) uvažujme o relativistickej hmotnosti mr miesto hmotnosti m. Ak vypočítanú rýchlosť a vzťahom (10.1.1.1.6) vypočítanú relativistickú hmotnosť dosadíme do vzťahu (10.1.1.1.3), po úpravách a výpočtoch aj priemerný študent získa hodnotu polomeru kružnice a frekvenciu pohybu relativistického elektrónu po kružnici. Vzťahy relativistickej fyziky degenerujú do vzťahov klasickej fyziky a dávajú tie isté výsledky, ak je pomer kinetickej energie a „pokojovej“ energie mc2 zanedbateľný v porovnaní s číslom 1. V našom prípade

preto máme právo použiť vzťahy klasickej fyziky.

Príklad 10.1.1.2

Aký je polomer r a aké je stúpanie p skrutkovice, po ktorej sa pohybuje elektrón rýchlosťou v veľkosti v = c/100 v homogénnom magnetickom poli s magnetickou indukciou veľkosti B = 1 T tak, že uhol j medzi smerom rýchlosti v a smerom magnetickej indukcie B je 80°? Elektrický náboj elektrónu je q = -1,602.10^-19 C, hmotnosť elektrónu je m= 9,11.10^-31 kg, rýchlosť svetla vo vákuu je c = 3.10⁸ m/s.

Riešenie 

Keďže veľkosť rýchlosti elektrónu v je 100-krát menšia než rýchlosť svetla vo vákuu c, relativistický prírastok hmotnosti elektrónu zanedbáme. Rýchlosť v môžeme rozložiť na zložku v_k kolmú na magnetickú indukciu B a zložku v_r rovnobežnú so smerom magnetickej indukcie B. Magnetická sila F_m je podľa (10.1.1.2) kolmá na magnetickú indukciu B. Keďže v smere magnetickej indukcie B nepôsobí na elektrón žiadna sila, zachováva sa zložka rýchlosti v_r . Pozorovateľ spriahnutý s rovinou kolmou na magnetickú indukciu B pozoruje v tejto rovine pohyb elektrónu po kružnici s polomerom r, pretože magnetická sila F_m pôsobí na elektrón kolmo na zložku rýchlosti v_k ležiacu v tejto rovine. Vonkajší pozorovateľ pozoruje superpozíciu oboch pohybov – pohyb po skrutkovici s polomerom r. Od veľkosti vsin j zložky rýchlosti v_k závisí veľkosť dostredivej sily F a polomer r skrutkovice. Úlohu dostredivej sily F zohráva magnetická sila F_m, preto porovnaním ich veľkostí dostaneme

a po úprave získame vzťah pre polomer r skrutkovice

(10.1.1.2.1)

Zrejme elektrón prejde po jednom závite skrutkovice za ten istý čas T, za ktorý prejde priemet elektrónu na rovinu kolmú na magnetickú indukciu B raz po kružnici s polomerom r rýchlosťou vsin j . S využitím (10.1.1.2.1) získame

Od veľkosti vcos j rovnobežnej zložky v_r rýchlosti závisí stúpanie p skrutkovice, čo je vzdialenosť medzi dvomi susednými závitmi skrutkovice

(10.1.1.2.2)

Po dosadení zadaných hodnôt do vzťahov (10.1.1.2.1), (10.1.1.2.2) dostaneme

Polomer skrutkovice je 16,8 mm, stúpanie skrutkovice je 18,6 mm. Elektrón pri pohybe zatáča smer svojej rýchlosti doľava.