 Ampérov zákon celkového prúdu
Ampérov zákon celkového prúdu
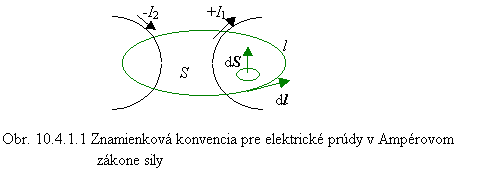
V podkapitole 10.1 sa konštatuje, že stacionárne magnetické (magnetostatické) pole je vyvolané stacionárnym prúdovým poľom. Stacionárne prúdové pole sa nachádza vo vodičoch s jednosmernými elektrickými prúdmi. Predpokladajme, že sa vo vákuu nachádzajú prúdovodiče ľubovoľného tvaru. V ich okolí existuje magnetické pole. Ampérov zákon celkového prúdu stanovuje väzbu medzi elektrickými prúdmi a magnetickým poľom, ktoré tieto prúdy vyvolali: krivkový integrál magnetickej indukcie B po ľubovoľnej uzavretej orientovanej krivke l je priamoúmerný celkovému elektrickému prúdu Ic, ktorý tečie cez ľubovoľný povrch S ohraničený touto krivkou, pozri obr. 10.4.1.1.
![]() (10.4.1.1)
(10.4.1.1)
Celkový elektrický prúd sa rovná algebraickému súčtu prúdov, ktoré tečú cez ľubovoľný povrch S ohraničený touto krivkou. Elektrickému prúdu, ktorý tečie cez povrch S v smere vztýčeného palca pravej ruky, ak ohnuté prsty ukazujú smer integrovania (smer vektora dl) po krivke l, priradíme znamienko plus, v opačnom prípade mu priradíme znamienko mínus.
V prípade nestacionárnych elektrických polí bude tiecť cez povrch natiahnutý na uzavretú integračnú krivku l aj Maxwellov posuvný prúd Ip
![]() (10.4.1.2)
(10.4.1.2)
kde Y je elektrický indukčný tok cez povrch S ohraničený uzavretou integračnou krivkou l
![]()
Smer vektora dS je určený pravidlom pravej ruky, pozri obr. 10.4.1.1.
V tomto prípade má Ampérov zákon tvar
![]() (10.4.1.3)
(10.4.1.3)
Magnetická konštanta (permeabilita vákua) m0 má zrejme rozmer T.m/A = (T.m2)/(A.m) = (Wb/A)/m = H/m, weber (Wb) je jednotkou magnetického toku, henry (H) je jednotkou indukčnosti. Veličiny magnetický tok a indukčnosť budú definované neskôr. V sústave jednotiek SI má magnetická konštanta hodnotu
![]()
V úlohách s rovinnou, valcovou a guľovou symetriou nám Ampérov zákon umožňuje z hodnoty krivkového integrálu priamo určiť magnetickú indukciu B v požadovaných bodoch vo vákuu.
Príklad 10.4.1.1
Vypočítajte priemet magnetickej indukcie na myslenú kružnicu s polomerom r = 10 cm, pričom nekonečne dlhý priamy vodič s prúdom I = 2 A prechádza stredom kružnice kolmo na rovinu kružnice. Vodič sa nachádza vo vákuu. Má kruhový prierez polomeru R = 1 cm.
Riešenie
Úloha má zjavnú valcovú symetriu, preto veľkosť B magnetickej indukcie musí byť rovnaká na povrchu plášťa valca polomeru r, ak je na osi valca uložený prúdovodič. Uzavretú integračnú krivku l zvolíme v tvare kružnice polomeru r, body ktorej ležia na plášti valca. Smer integrovania určíme pravidlom pravej ruky - v smere zahnutých prstov pravej ruky ak palec ukazuje smer elektrického prúdu vo vodiči. Pri tejto orientácii sú obe strany vzťahu (10.4.1.1) kladné, a preto prsty pravej ruky ukazujú smer magnetickej indukcie B na integračnej kružnici l. Z valcovej symetrie vyplýva, že veľkosť priemetu magnetickej indukcie bude v každom bode kružnice rovnaká.
![]()
Po zrejmej úprave dostaneme
![]() (10.4.1.1.1)
(10.4.1.1.1)
Po dosadení zadaných hodnôt dostaneme
![]()
Veľkosť priemetu magnetickej indukcie na kružnicu bude 4 mT.
Príklad 10.4.1.2
Vypočítajte magnetickú indukciu na kruhovej osi dutiny toroidu polomeru r = 10 cm, s počtom závitov N = 400. Toroidom (do kruhu stočeným solenoidom) tečie prúd I = 2 A. Toroid sa nachádza vo vákuu.
Riešenie
Úloha má zjavnú symetriu a magnetické indukčné čiary v dutine toroidu majú tvar kružníc. Smer magnetickej indukcie v dutine toroidu určíme pravidlom pravej ruky: ak uchopíme časť toroidu do pravej ruky tak, aby zahnuté prsty ukazovali smer prúdu v závitoch toroidu, vychýlený palec ukáže smer magnetickej indukcie na magnetickej indukčnej čiare vnútri toroidu. Ak v tomto smere integrujeme magnetickú indukciu na uzavretej kruhovej osi dutiny, s využitím Ampérovho zákona získame
![]()
Po zrejmej úprave dostaneme
![]() (10.4.1.2.1)
(10.4.1.2.1)
Po dosadení zadaných hodnôt dostaneme
![]()
Veľkosť magnetickej indukcie bude 1,6 mT, smer určíme pravidlom pravej ruky.

